使用keras搭建神经网络

阅读：1234299 分享到

Keras 是一个高层神经网络库，Keras 由纯 Python 编写而成并基 Tensorflow 或 Theano。Keras 为支持快速实验而生，能够把你的 idea 迅速转换为结果。

Tensorflow 2.0 已经与 Keras 深度进行了融合，我们既可以用 Keras 的高级接口迅速搭建和训练模型。

六步骤法

使用 keras 搭建神经网络遵循 6 步法：

第1步（import）：import 需要的模块。

第2步（train,test）：告知要喂入网络的训练集和测试集是什么，也就是训练集的特征值和标签（x_train,y_train）以及训练集的特征值和标签（x_test,y_test）。

第3步（model=tf.keras.models.Squential）：在 Sequential 中搭建网络结构，逐层描述每层网络，也就是实现前向传播。

第4步（model.compile）：在 compile 中配置训练方法，告知训练时使用哪种优化器，选择哪个损失函数，选择哪种评测指标。

第5步（model.fit）：在fit中执行训练过程，告知训练集和测试集的输入特征和标签，告知每个 batch 是多少，告知要迭代多少次数据集。

第6步（model.summary）：使用 summary 打印出网络的结构和参数统计。

keras 函数详解

以后我们搭建神经网络就按照上面的六步法则进行编写代码，接下来我们来学习 keras 提供的这些函数的用法。

Sequential 可以认为是个容器，这个容器里面封装了一个神经网络结构，我们可以使用 Sequential 描述从输入层到输出层每一层的网络结构，每一层的网络结构可以是一下几种。

1.拉直层：tf.keras.layers.Flatten()。有时候我们从第三方机构获取的数据集特征值是二维的（比如图片特征值），我们可以使用该函数把矩阵转换为一维向量。

2.全连接层：tf.keras.layers.Dense(神经元个数，activation=“激活函数”,kernel_regularizer=正则化）。其中 activation 以字符串给出，可以使用的激活函数有 relu、softmox、sigmod、tanh等；其中 kernel_regularizer 填入函数名，我们可以使用 l1 正则化和 l2 正则化，分别使用函数 tf.eras.regularizers.l1()、tf.keras.regularizers.l2()。

3.卷积层：tf.keras.layers.Conv2D(filers=卷积核个数,kernel_size=卷积核尺寸,strides=卷积步长,padding=“valid”or“same”)。卷积层的知识我们后面再介绍。

4.LSTM层：tf.keras.layers.LSTM()。循环网络层的知识我们后面再介绍。

Model.compile(optimizer=优化器，loss=损失函数，metrics=[“准确率”]）函数配置神经网络的训练方法，我们在 compile 函数的参数中设置训练时选择的优化器、损失函数和评测指标，其中优化器和损失函数可以是以字符串的形式给出也可以以函数的形式给出。

优化器 Optimizer 的选择有以下几种：

1.‘sgd’ or tf.keras.optimizers.SGD (lr=学习率,momentum=动量参数)

2.‘adagrad’ or tf.keras.optimizers.Adagrad (lr=学习率)

3.‘adadelta’ or tf.keras.optimizers.Adadelta (lr=学习率)

4.‘adam’ or tf.keras.optimizers.Adam (lr=学习率, beta_1=0.9, beta_2=0.999)

损失函数 loss 的选择有以下几种：

1.‘mse’ or tf.keras.losses.MeanSquaredError()

2.‘sparse_categorical_crossentropy’ or tf.keras.losses.SparseCategoricalCrossentropy(from_logits=False)

使用 keras 高阶 API 训练神经网络时，我们常使用第二种损失函数，该函数有个 from_logits 参数，如果神经网络使用了 softmax 使得输出符合概率分布或使用 sigmod 使得输出分布在 [0,1] 之间，该参数设置为 False，否则该参数设置为 True。

网络评测指标 metrics 的选择有以下几种：

1.‘accuracy’：y_和y都是数值，如y_=[1] y=[1]

2.‘categorical_accuracy’：y_和y都是独热码(概率分布)，如y_=[0,1,0] y=[0.256,0.695,0.048]

3.‘sparse_categorical_accuracy’：y_是数值，y是独热码(概率分布)或(0, 1)之间的值,如y_=[1] y=[0.256,0.695,0.048]

我们从第三方获取的数据集大都是以数值形式给出标签的值，比如前面使用的鸢尾花数据集的标签，而我们在训练神经网络时，对于单分类问题我们通常都会把前向传播的输出使用 softmax 激活函数映射为符合概率分布的结果，对于多分类问题我们一般则使用 sigmod 激活函数把前向传播的输出映射到(0, 1)之间，所以 metrics 参数的值我们一般都是用第 3 种；如果你想使用第 2 种，则需要自己使用 one_hot 函数把标签转为独热码形式。

model.fit（训练集的输入特征，训练集的标签，batch_size=，epochs=，validation_data=(测试集的输入特征，测试集的标签）,validation_split=从训练集划分多少比例给测试集，validation_freq=多少次epoch测试一次），其中 validation_data 和 validation_split 只需要使用一个。

model.summary 可以打印出网络的结构和参数统计，如下图是我们前面的鸢尾花分类的输出结果，该网络结构为 4 个输入（4 个特征值），3 个输出（标签 3 分类）的一层网络（一个 w），dense 全连接共有 15 个参数（参数 w 是 4 行 3 列共 12 个元素，参数 b 是 3 个元素的向量，共 15 个参数），Trainable params 是可训练参数共有 15 个，Non-trainable 是不可训练参数有 0 个。

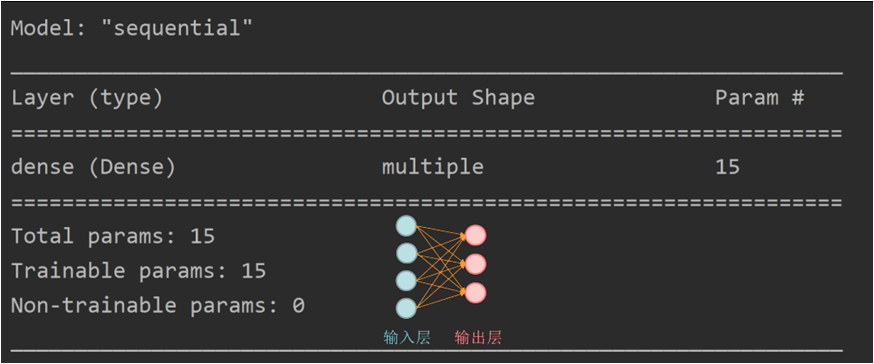
keras 实现鸢尾花分类

下面我们使用 keras 的 6 步法编写代码来实现鸢尾花分类。

import tensorflow as tf
from sklearn import datasets
import numpy as np

x_train = datasets.load_iris().data
y_train = datasets.load_iris().target
np.random.seed(1024)
np.random.shuffle(x_train)
np.random.seed(1024)
np.random.shuffle(y_train)

'''
1.目前我们使用1层神经网络，所以共有3个神经元（输出层3分类所以是3个神经元，输入层不做计算不是神经元）
2.激活函数使用softmax使得结果符合概率分布
3.正则化使用l2正则化
4.Sequential参数是个list，本案例我们只使用1层神经网络，所以list填入1个dense，如果你使用多层神经网络
则需要在list中增加隐藏层的dense。
'''
model = tf.keras.models.Sequential([
    tf.keras.layers.Dense(3, activation="softmax", kernel_regularizer=tf.keras.regularizers.l2())
])


'''
1.优化器使用SGD，学习率设置为0.1
2.激活函数使用softmax使得结果符合概率分布，所以from_logits=False
3.鸢尾花数据集的标签是数值，我们前向传播结果是独热码符合概率分布
'''
model.compile(optimizer=tf.keras.optimizers.SGD(lr=0.1),
              loss=tf.keras.losses.SparseCategoricalCrossentropy(from_logits=False),
              metrics=["sparse_categorical_accuracy"])

'''
1.x_train是训练特征值，y_train是训练标签
2.batch_size：每次喂入神经网络32组数据
3.epochs：迭代循环次数500
4.validation_split：从训练集的20%作为测试集
5.validation_freq：每迭代20次从测试集中验证一次准确率
'''
model.fit(x_train, y_train, batch_size=32, epochs=100, validation_split=0.2, validation_freq=20)

# 打印出神经网络结构和参数
model.summary()

代码运行结果如下：

4/4 [==============================] - 0s 5ms/step - loss: 1.6351 - sparse_categorical_accuracy: 0.2417
Epoch 2/100
4/4 [==============================] - 0s 1ms/step - loss: 1.3186 - sparse_categorical_accuracy: 0.4250
Epoch 3/100
4/4 [==============================] - 0s 2ms/step - loss: 1.1365 - sparse_categorical_accuracy: 0.6583
Epoch 4/100
4/4 [==============================] - 0s 2ms/step - loss: 0.8764 - sparse_categorical_accuracy: 0.6667
Epoch 5/100
4/4 [==============================] - 0s 2ms/step - loss: 1.1204 - sparse_categorical_accuracy: 0.5500
Epoch 6/100
4/4 [==============================] - 0s 2ms/step - loss: 0.7333 - sparse_categorical_accuracy: 0.6417
Epoch 7/100
4/4 [==============================] - 0s 1ms/step - loss: 0.8290 - sparse_categorical_accuracy: 0.7000
Epoch 8/100
4/4 [==============================] - 0s 2ms/step - loss: 0.8973 - sparse_categorical_accuracy: 0.6333
Epoch 9/100
4/4 [==============================] - 0s 1ms/step - loss: 0.6544 - sparse_categorical_accuracy: 0.6750
Epoch 10/100
4/4 [==============================] - 0s 2ms/step - loss: 0.6212 - sparse_categorical_accuracy: 0.7083
Epoch 11/100
4/4 [==============================] - 0s 1000us/step - loss: 0.7828 - sparse_categorical_accuracy: 0.6667
Epoch 12/100
4/4 [==============================] - 0s 2ms/step - loss: 0.9137 - sparse_categorical_accuracy: 0.7000
Epoch 13/100
4/4 [==============================] - 0s 1ms/step - loss: 0.5994 - sparse_categorical_accuracy: 0.7167
Epoch 14/100
4/4 [==============================] - 0s 2ms/step - loss: 0.4895 - sparse_categorical_accuracy: 0.9083
Epoch 15/100
4/4 [==============================] - 0s 1ms/step - loss: 0.6755 - sparse_categorical_accuracy: 0.7167
Epoch 16/100
4/4 [==============================] - 0s 1ms/step - loss: 0.9959 - sparse_categorical_accuracy: 0.6500
Epoch 17/100
4/4 [==============================] - 0s 1ms/step - loss: 0.6598 - sparse_categorical_accuracy: 0.8250
Epoch 18/100
4/4 [==============================] - 0s 1ms/step - loss: 0.4618 - sparse_categorical_accuracy: 0.9250
Epoch 19/100
4/4 [==============================] - 0s 1ms/step - loss: 0.4634 - sparse_categorical_accuracy: 0.8333
Epoch 20/100
4/4 [==============================] - 0s 108ms/step - loss: 0.6006 - sparse_categorical_accuracy: 0.6750 - val_loss: 0.4201 - val_sparse_categorical_accuracy: 0.8000
Epoch 21/100
4/4 [==============================] - 0s 1ms/step - loss: 0.5555 - sparse_categorical_accuracy: 0.7083
Epoch 22/100
4/4 [==============================] - 0s 1ms/step - loss: 0.4485 - sparse_categorical_accuracy: 0.8750
Epoch 23/100
4/4 [==============================] - 0s 1ms/step - loss: 0.6362 - sparse_categorical_accuracy: 0.7000
Epoch 24/100
4/4 [==============================] - 0s 1ms/step - loss: 0.5023 - sparse_categorical_accuracy: 0.8333
Epoch 25/100
4/4 [==============================] - 0s 1ms/step - loss: 0.4327 - sparse_categorical_accuracy: 0.8667
Epoch 26/100
4/4 [==============================] - 0s 2ms/step - loss: 0.4627 - sparse_categorical_accuracy: 0.8083
Epoch 27/100
4/4 [==============================] - 0s 1ms/step - loss: 0.6103 - sparse_categorical_accuracy: 0.7000
Epoch 28/100
4/4 [==============================] - 0s 1ms/step - loss: 0.5095 - sparse_categorical_accuracy: 0.8333
Epoch 29/100
4/4 [==============================] - 0s 1ms/step - loss: 0.4225 - sparse_categorical_accuracy: 0.8917
Epoch 30/100
4/4 [==============================] - 0s 2ms/step - loss: 0.4350 - sparse_categorical_accuracy: 0.8917
Epoch 31/100
4/4 [==============================] - 0s 1ms/step - loss: 0.4355 - sparse_categorical_accuracy: 0.9167
Epoch 32/100
4/4 [==============================] - 0s 1ms/step - loss: 0.5568 - sparse_categorical_accuracy: 0.7917
Epoch 33/100
4/4 [==============================] - 0s 750us/step - loss: 0.4678 - sparse_categorical_accuracy: 0.8667
Epoch 34/100
4/4 [==============================] - 0s 1ms/step - loss: 0.6253 - sparse_categorical_accuracy: 0.7000
Epoch 35/100
4/4 [==============================] - 0s 1ms/step - loss: 0.4059 - sparse_categorical_accuracy: 0.9583
Epoch 36/100
4/4 [==============================] - 0s 1ms/step - loss: 0.5605 - sparse_categorical_accuracy: 0.7583
Epoch 37/100
4/4 [==============================] - 0s 2ms/step - loss: 0.5138 - sparse_categorical_accuracy: 0.7250
Epoch 38/100
4/4 [==============================] - 0s 1ms/step - loss: 0.4304 - sparse_categorical_accuracy: 0.9000
Epoch 39/100
4/4 [==============================] - 0s 1ms/step - loss: 0.5555 - sparse_categorical_accuracy: 0.7417
Epoch 40/100
4/4 [==============================] - 0s 14ms/step - loss: 0.6257 - sparse_categorical_accuracy: 0.7750 - val_loss: 0.3507 - val_sparse_categorical_accuracy: 0.9667
Epoch 41/100
4/4 [==============================] - 0s 6ms/step - loss: 0.5206 - sparse_categorical_accuracy: 0.7500
Epoch 42/100
4/4 [==============================] - 0s 3ms/step - loss: 0.4249 - sparse_categorical_accuracy: 0.8250
Epoch 43/100
4/4 [==============================] - 0s 1ms/step - loss: 0.4254 - sparse_categorical_accuracy: 0.8917
Epoch 44/100
4/4 [==============================] - 0s 5ms/step - loss: 0.8867 - sparse_categorical_accuracy: 0.5917
Epoch 45/100
4/4 [==============================] - 0s 2ms/step - loss: 0.7229 - sparse_categorical_accuracy: 0.6750
Epoch 46/100
4/4 [==============================] - 0s 4ms/step - loss: 0.5368 - sparse_categorical_accuracy: 0.7917
Epoch 47/100
4/4 [==============================] - 0s 2ms/step - loss: 0.4386 - sparse_categorical_accuracy: 0.8583
Epoch 48/100
4/4 [==============================] - 0s 1ms/step - loss: 0.4074 - sparse_categorical_accuracy: 0.9250
Epoch 49/100
4/4 [==============================] - 0s 4ms/step - loss: 0.3923 - sparse_categorical_accuracy: 0.9250
Epoch 50/100
4/4 [==============================] - 0s 2ms/step - loss: 0.4920 - sparse_categorical_accuracy: 0.8167
Epoch 51/100
4/4 [==============================] - 0s 1ms/step - loss: 0.4358 - sparse_categorical_accuracy: 0.8250
Epoch 52/100
4/4 [==============================] - 0s 2ms/step - loss: 0.5347 - sparse_categorical_accuracy: 0.7250
Epoch 53/100
4/4 [==============================] - 0s 3ms/step - loss: 0.3951 - sparse_categorical_accuracy: 0.9167
Epoch 54/100
4/4 [==============================] - 0s 3ms/step - loss: 0.4206 - sparse_categorical_accuracy: 0.8750
Epoch 55/100
4/4 [==============================] - 0s 12ms/step - loss: 0.4214 - sparse_categorical_accuracy: 0.8500
Epoch 56/100
4/4 [==============================] - 0s 14ms/step - loss: 0.3791 - sparse_categorical_accuracy: 0.9500
Epoch 57/100
4/4 [==============================] - 0s 5ms/step - loss: 0.4462 - sparse_categorical_accuracy: 0.8667
Epoch 58/100
4/4 [==============================] - 0s 16ms/step - loss: 0.3880 - sparse_categorical_accuracy: 0.9083
Epoch 59/100
4/4 [==============================] - 0s 19ms/step - loss: 0.4217 - sparse_categorical_accuracy: 0.8750
Epoch 60/100
4/4 [==============================] - 0s 105ms/step - loss: 0.3733 - sparse_categorical_accuracy: 0.9333 - val_loss: 0.4586 - val_sparse_categorical_accuracy: 0.7667
Epoch 61/100
4/4 [==============================] - 0s 1ms/step - loss: 0.4252 - sparse_categorical_accuracy: 0.8667
Epoch 62/100
4/4 [==============================] - 0s 7ms/step - loss: 0.4210 - sparse_categorical_accuracy: 0.8583
Epoch 63/100
4/4 [==============================] - 0s 2ms/step - loss: 0.4720 - sparse_categorical_accuracy: 0.8083
Epoch 64/100
4/4 [==============================] - 0s 1ms/step - loss: 0.3808 - sparse_categorical_accuracy: 0.9333
Epoch 65/100
4/4 [==============================] - 0s 2ms/step - loss: 0.5067 - sparse_categorical_accuracy: 0.7833
Epoch 66/100
4/4 [==============================] - 0s 3ms/step - loss: 0.4058 - sparse_categorical_accuracy: 0.8833
Epoch 67/100
4/4 [==============================] - 0s 1ms/step - loss: 0.4304 - sparse_categorical_accuracy: 0.8417
Epoch 68/100
4/4 [==============================] - 0s 1ms/step - loss: 0.4292 - sparse_categorical_accuracy: 0.8583
Epoch 69/100
4/4 [==============================] - 0s 750us/step - loss: 0.5901 - sparse_categorical_accuracy: 0.7083
Epoch 70/100
4/4 [==============================] - 0s 4ms/step - loss: 0.3781 - sparse_categorical_accuracy: 0.9500
Epoch 71/100
4/4 [==============================] - 0s 2ms/step - loss: 0.3938 - sparse_categorical_accuracy: 0.9167
Epoch 72/100
4/4 [==============================] - 0s 1ms/step - loss: 0.3954 - sparse_categorical_accuracy: 0.9083
Epoch 73/100
4/4 [==============================] - 0s 3ms/step - loss: 0.4345 - sparse_categorical_accuracy: 0.8333
Epoch 74/100
4/4 [==============================] - 0s 2ms/step - loss: 0.4539 - sparse_categorical_accuracy: 0.8250
Epoch 75/100
4/4 [==============================] - 0s 10ms/step - loss: 0.4821 - sparse_categorical_accuracy: 0.7917
Epoch 76/100
4/4 [==============================] - 0s 2ms/step - loss: 0.3892 - sparse_categorical_accuracy: 0.9250
Epoch 77/100
4/4 [==============================] - 0s 15ms/step - loss: 0.3969 - sparse_categorical_accuracy: 0.8750
Epoch 78/100
4/4 [==============================] - 0s 3ms/step - loss: 0.5736 - sparse_categorical_accuracy: 0.7750
Epoch 79/100
4/4 [==============================] - 0s 3ms/step - loss: 0.3861 - sparse_categorical_accuracy: 0.9000
Epoch 80/100
4/4 [==============================] - 0s 47ms/step - loss: 0.3713 - sparse_categorical_accuracy: 0.9583 - val_loss: 0.3176 - val_sparse_categorical_accuracy: 1.0000
Epoch 81/100
4/4 [==============================] - 0s 2ms/step - loss: 0.4649 - sparse_categorical_accuracy: 0.8167
Epoch 82/100
4/4 [==============================] - 0s 2ms/step - loss: 0.4421 - sparse_categorical_accuracy: 0.8583
Epoch 83/100
4/4 [==============================] - 0s 2ms/step - loss: 0.5516 - sparse_categorical_accuracy: 0.7583
Epoch 84/100
4/4 [==============================] - 0s 2ms/step - loss: 0.4063 - sparse_categorical_accuracy: 0.9083
Epoch 85/100
4/4 [==============================] - 0s 2ms/step - loss: 0.3740 - sparse_categorical_accuracy: 0.9333
Epoch 86/100
4/4 [==============================] - 0s 2ms/step - loss: 0.3908 - sparse_categorical_accuracy: 0.9417
Epoch 87/100
4/4 [==============================] - 0s 1ms/step - loss: 0.3956 - sparse_categorical_accuracy: 0.9417
Epoch 88/100
4/4 [==============================] - 0s 2ms/step - loss: 0.3925 - sparse_categorical_accuracy: 0.9000
Epoch 89/100
4/4 [==============================] - 0s 2ms/step - loss: 0.3834 - sparse_categorical_accuracy: 0.9167
Epoch 90/100
4/4 [==============================] - 0s 2ms/step - loss: 0.4654 - sparse_categorical_accuracy: 0.7917
Epoch 91/100
4/4 [==============================] - 0s 2ms/step - loss: 0.4126 - sparse_categorical_accuracy: 0.9083
Epoch 92/100
4/4 [==============================] - 0s 1ms/step - loss: 0.6133 - sparse_categorical_accuracy: 0.7083
Epoch 93/100
4/4 [==============================] - 0s 1ms/step - loss: 0.4386 - sparse_categorical_accuracy: 0.8333
Epoch 94/100
4/4 [==============================] - 0s 2ms/step - loss: 0.3646 - sparse_categorical_accuracy: 0.9500
Epoch 95/100
4/4 [==============================] - 0s 3ms/step - loss: 0.3656 - sparse_categorical_accuracy: 0.9667
Epoch 96/100
4/4 [==============================] - 0s 1ms/step - loss: 0.3967 - sparse_categorical_accuracy: 0.9167
Epoch 97/100
4/4 [==============================] - 0s 2ms/step - loss: 0.5092 - sparse_categorical_accuracy: 0.7667
Epoch 98/100
4/4 [==============================] - 0s 3ms/step - loss: 0.3876 - sparse_categorical_accuracy: 0.9250
Epoch 99/100
4/4 [==============================] - 0s 4ms/step - loss: 0.4302 - sparse_categorical_accuracy: 0.8333
Epoch 100/100
4/4 [==============================] - 0s 90ms/step - loss: 0.3709 - sparse_categorical_accuracy: 0.8917 - val_loss: 0.3749 - val_sparse_categorical_accuracy: 0.9333
Model: "sequential"
_________________________________________________________________
Layer (type)                 Output Shape              Param #
=================================================================
dense (Dense)                multiple                  15
=================================================================
Total params: 15
Trainable params: 15
Non-trainable params: 0
_________________________________________________________________

通过 model.summary 打印出我们搭建的神经网络的结构和参数统计，该网络结构为 4 个输入（4 个特征值），3 个输出（标签 3 分类）的一层网络（一个 w），dense 全连接共有 15 个参数（参数 w 是 4 行 3 列共 12 个元素，参数 b 是 3 个元素的向量，共 15 个参数），Trainable params 是可训练参数共有 15 个，Non-trainable 是不可训练参数有 0 个。

在类里面使用 keras 实现鸢尾花分类

下面我们在类里面使用 keras 的六步法编写代码来实现鸢尾花分类。

import tensorflow as tf
from tensorflow.keras.layers import Dense
from tensorflow.keras import Model
from sklearn import datasets
import numpy as np

x_train = datasets.load_iris().data
y_train = datasets.load_iris().target

np.random.seed(1024)
np.random.shuffle(x_train)
np.random.seed(1024)
np.random.shuffle(y_train)
tf.random.set_seed(1024)

class IrisModel(Model):
    def __init__(self):
        super(IrisModel, self).__init__()
        self.d1 = Dense(3, activation='softmax', kernel_regularizer=tf.keras.regularizers.l2())

    def call(self, x):
        # 在call函数中调用self.d1实现了从输入x到出y的前向传播
        y = self.d1(x)
        return y


model = IrisModel()
model.compile(optimizer=tf.keras.optimizers.SGD(lr=0.1),
              loss=tf.keras.losses.SparseCategoricalCrossentropy(from_logits=False),
              metrics=['sparse_categorical_accuracy'])

model.fit(x_train, y_train, batch_size=32, epochs=500, validation_split=0.2, validation_freq=20)
model.summary()

代码运行的结果和上面一致，通过 model.summary 打印出的网络结构也是一样的，大家可以自行试验。

如果神经网络有多层，我们只需要在构造函数中定义多个 Dense 即可，我们在 call 函数中调用相应的 Dense 实现前向传播，model.fit 中会不停的调用对象中的 call 函数（函数对象）。其余写法和我们前面一致。

sigmod 和 softmax 的区别

网上代码案例中同学们可能看到有的分类问题使用激活函数 sigmod 有的使用激活函数 softmax，总是分不清这两者有什么区别，在此我们就来讲解一下这两者的区别。

sigmoid=多标签分类问题=多个正确答案=非独占输出（例如胸部X光检查、住院）。构建分类器，解决有多个正确答案的问题时，用 sigmoid 函数分别处理各个原始输出值，sigmoid 函数是一种 logistic 函数，它将任意的值转换到 (0,1)之间，但这些值之间没有关联，都是属于独立分布。

softmax=多类别分类问题=只有一个正确答案=互斥输出（例如手写数字，鸢尾花）。构建分类器，解决只有唯一正确答案的问题时，用 softmax 函数处理各个原始输出值，它将任意的值转换到 (0,1)之间。softmax 函数的分母综合了原始输出值的所有因素，这意味着，softmax 函数得到的不同概率之间相互关联，而这些值的累和为1（满足概率的性质）。

如果模型输出为非互斥类别，且可以同时选择多个类别，则采用 sigmoid 函数计算该网络的原始输出值。如果模型输出为互斥类别，且只能选择一个类别，则采用 softmax 函数计算该网络的原始输出值。sigmoid 函数可以用来解决多标签问题，softmax 函数用来解决单标签问题。对于某个分类场景，当 softmax 函数能用时，sigmoid 函数一定可以用。

假设有一个前向传播的输出为：[-0.9419267177581787, 1.944047451019287]，对应的类别分别为(0, 1)，这个属于分类结果唯一，我们分别使用 sigmod 和 softmax 激活函数运算，代码如下：

import tensorflow as tf

y = tf.constant([-0.9419267177581787, 1.944047451019287])
print(tf.nn.sigmoid(y))
print(tf.nn.softmax(y))

程序运行结果如下：

tf.Tensor([0.28051132 0.8747961 ], shape=(2,), dtype=float32)
tf.Tensor([0.05285128 0.9471487 ], shape=(2,), dtype=float32)

我们经过 sigmoid 运算的结果为：[0.2805, 0.8748]。前者 0.2805 指的是分类类别为 0 的概率；0.8748 指的是分类类别为 1 的概率。二者相互独立，可看作两次独立的实验（显然在这里不适用，因为 0-1 类别之间显然不是相互独立的两次伯努利事件）。所以显而易见的，二者加和并不等于 1。

我们经过 softmax 运算的结果为 [0.0529, 0.9471]，这里两者加和是 1，对于分类结果唯一的问题，我们使用 softmax 函数明显更精确。

假设有一个前向传播的输出为：[-0.9, 1.9, 0.3,1.5]，对应的类别分别为(0, 1 , 0 , 1)，这个属于分类结果不唯一，我们分别使用 sigmod 和 softmax 激活函数运算，代码如下：

import tensorflow as tf

y = tf.constant([-0.9, 1.9, 0.3, 1.5])
print(tf.nn.sigmoid(y))
print(tf.nn.softmax(y))

程序运行的结果如下：

tf.Tensor([0.2890505  0.8698916  0.5744425  0.81757444], shape=(4,), dtype=float32)
tf.Tensor([0.03145847 0.51732343 0.10444581 0.34677225], shape=(4,), dtype=float32)

从结果上看，使用 sigmod 的效果更好。

本节重要知识点

会使用 keras 搭建神经网络

会使用类的方法编写代码

了解 sigmod 和 softmax 使用场景

如果以上内容对您有帮助，请老板用微信扫一下赞赏码，赞赏后加微信号 birdpython 领取免费视频。

请登录后评论