正则化
阅读：1322656786 分享到
在神经网络学习过程中，如果模型对现有数据集学习的不够彻底，就会导致训练出来的神经网络模型不能有效的拟合数据集，使得模型学不到什么东西，该模型就如一个学渣一样；如果模型对现有数据集学习的比较死板，就会导致训练出来的神经网络模型缺乏泛化力，使得模型对从未见过的新数据就难以准确的预测，该模型就如一个只会死读书的书呆子一样；我们希望神经网络模型的学习方法得当，能达到举一反三的能力也就是恰当拟合，该模型就如一个学霸一样。三种拟合模型的结构图如下。
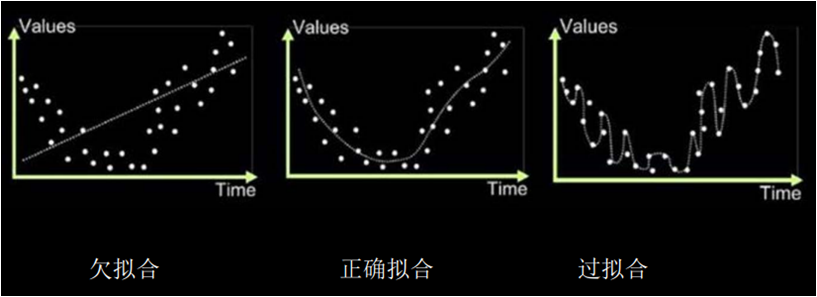
正则化的特点
缓解欠拟合：
1.增加数据集特征项，给网络更多维度的输入特征。（增加输入特征值）
2.扩展网络规模增加网络深度来提升模型表达力。（增加网络参数w，b等）
3.减少正则化参数。
缓解过拟合：
1.对数据进行清洗，减少数据集中的噪声，使数据集更纯净。（数据清洗）
2.增加训练集让模型学到更多的数据。（多学点，以便找到规律）
3.采用正则化和增大正则化参数。
欠拟合主要原因是学习不足，欠拟合问题非常好解决，我们一般是增加数据集的特征和扩展网络参数即可。
对于过拟合问题，数据清洗和增加数据集，我们一般也可以很好的解决，在此我们讲解一下正则化是什么。
在缓解过拟合的方法中，正则化是一种通用的有效方法，正则化就是在损失函数中引入模型复杂度指标，给每个参数w加上权重来抑制训练数据集中的噪声，正则化通常只对参数 w 使用，我们一般不正则化 b。
L1 正则化和 L2 正则化
使用正则化后，让原来的损失函数公式 loss 加上一项成为一个新的 loss 函数，然后我们使用这个新的 loss 函数来进行训练神经网络。
该公式中的第一部分我们已经非常熟悉了，是预测值和标准答案之间的差距，我们可以使用均方误差、自定义损失函数或者交叉熵来解决；第二个部分是参数 w 的权重，用超参数 REGULARIZER 给出参数 w 在总 loss 中的比重，其中 loss(w) 的计算公式可以使用两种方法。
第一个公式是对所有参数 w 的绝对值求和，我们叫做 L1 正则化；第二个公式是对所有参数 w 的平方求和，我们叫做 L2 正则化。
L1 正则化大概率会使很多参数变为零，因此该方法可通过稀疏参数 ，即减少参数的数量，降低复杂度；L2 正则化会使参数很接近零但不为零，因此该方法可通过减小参数值的大小降低复杂度。
在神经网络训练过程中，我们一般使用 L2 正则化，添加方式是，我们只需要改变 loss 函数的代码即可。
with tf.GradientTape() as tape: h1 = tf.matmul(x_train, w1) + b1 h1 = tf.nn.relu(h1) y = tf.matmul(h1, w2) + b2 loss_mse = tf.reduce_mean(tf.square(y_train - y)) # 均方误差作为损失函数 # 添加l2正则化 loss_regularization = [] loss_regularization.append(tf.nn.l2_loss(w1)) loss_regularization.append(tf.nn.l2_loss(w2)) loss_regularization = tf.reduce_sum(loss_regularization) loss = loss_mse + 0.03 * loss_regularization # REGULARIZER = 0.03
如上代码是一个 2 层神经网络的训练过程，我们在 loss 中加入 L2 正则化，也就是对 w 进行正则化。
本节重要知识点
了解什么是欠拟合和过拟合。
会使用 L2 正则化。
如果以上内容对您有帮助，请老板用微信扫一下赞赏码，赞赏后加微信号 birdpython 领取免费视频。
