



动态调整学习率
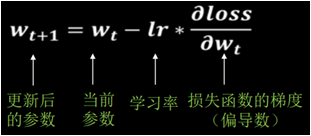
阅读:1233187933 分享到在前面的案例中,我们训练神经网络时,使用梯度下降的方法来使得损失函数变小,我们使用的参数更新公式如下图。公式中的lr为学习率,学习率代表在梯度下降过程中,参数每次更新的幅度。我们知道当学习率设置过小,参数更新过慢;如果设置过大,参数不收敛。

我们根据案例来分析学习率设置过小和过大的问题,假设有损失函数:loss = (w + 1)²,我们使用梯度下降的方法让损失函数 loss 的值逐渐趋向于 0,来更新 w。
学习率设置过小
我们首先给定学习率 lr 等于 0.01,然后进行训练,我们发现 loss 的值减少的很慢,代码如下。
import tensorflow as tf w = tf.Variable(tf.constant(5.0, dtype=tf.float32)) # 我们给w随机初始化一个值5.0 lr = 0.01 # 给定比较小的学习率 epoch = 20 # 学习训练20次 for step in range(epoch): # 迭代更新20次 with tf.GradientTape() as tape: loss = tf.square(w + 1) # 定义损失函数 loss=(w+1)² grads = tape.gradient(loss, w) # gradient函数让loss对w求导 w.assign_sub(lr * grads) # 更新w,使得:w = w -lr(∂loss/∂w) print("第 %s 次迭代后的w是 %f,对应的loss值是 %f" % (step + 1, w.numpy(), loss))
程序运行结果如下:
第 1 次迭代后的w是 4.880000,对应的loss值是 36.000000 第 2 次迭代后的w是 4.762400,对应的loss值是 34.574402 第 3 次迭代后的w是 4.647152,对应的loss值是 33.205254 第 4 次迭代后的w是 4.534209,对应的loss值是 31.890326 第 5 次迭代后的w是 4.423524,对应的loss值是 30.627466 第 6 次迭代后的w是 4.315054,对应的loss值是 29.414618 第 7 次迭代后的w是 4.208753,对应的loss值是 28.249798 第 8 次迭代后的w是 4.104578,对应的loss值是 27.131104 第 9 次迭代后的w是 4.002486,对应的loss值是 26.056711 第 10 次迭代后的w是 3.902436,对应的loss值是 25.024868 第 11 次迭代后的w是 3.804388,对应的loss值是 24.033882 第 12 次迭代后的w是 3.708300,对应的loss值是 23.082144 第 13 次迭代后的w是 3.614134,对应的loss值是 22.168091 第 14 次迭代后的w是 3.521851,对应的loss值是 21.290232 第 15 次迭代后的w是 3.431414,对应的loss值是 20.447142 第 16 次迭代后的w是 3.342786,对应的loss值是 19.637436 第 17 次迭代后的w是 3.255930,对应的loss值是 18.859789 第 18 次迭代后的w是 3.170812,对应的loss值是 18.112944 第 19 次迭代后的w是 3.087396,对应的loss值是 17.395670 第 20 次迭代后的w是 3.005648,对应的loss值是 16.706804
我们发现如果学习率给的过小,导致收敛慢,增加了训练的时间成本。
学习率设置过大
我们给定学习率 lr 等于 0.99,然后进行训练,我们发现 w 的值不收敛,代码如下。
import tensorflow as tf w = tf.Variable(tf.constant(5, dtype=tf.float32)) # 我们给w随机初始化一个值5.0 lr = 0.99 # 给定比较大的学习率 epoch = 20 # 学习训练20次 for step in range(epoch): # 迭代更新20次 with tf.GradientTape() as tape: loss = tf.square(w + 1) # 定义损失函数 loss=(w+1)² grads = tape.gradient(loss, w) # gradient函数让loss对w求导 w.assign_sub(lr * grads) # 更新w,使得:w = w -lr(∂loss/∂w) print("第 %s 次迭代后的w是 %f,对应的loss值是 %f" % (step + 1, w.numpy(), loss))
程序运行结果如下:
第 1 次迭代后的w是 -6.880000,对应的loss值是 36.000000 第 2 次迭代后的w是 4.762401,对应的loss值是 34.574402 第 3 次迭代后的w是 -6.647153,对应的loss值是 33.205261 第 4 次迭代后的w是 4.534210,对应的loss值是 31.890335 第 5 次迭代后的w是 -6.423526,对应的loss值是 30.627483 第 6 次迭代后的w是 4.315056,对应的loss值是 29.414633 第 7 次迭代后的w是 -6.208755,对应的loss值是 28.249819 第 8 次迭代后的w是 4.104580,对应的loss值是 27.131124 第 9 次迭代后的w是 -6.002488,对应的loss值是 26.056736 第 10 次迭代后的w是 3.902438,对应的loss值是 25.024887 第 11 次迭代后的w是 -5.804390,对应的loss值是 24.033899 第 12 次迭代后的w是 3.708302,对应的loss值是 23.082163 第 13 次迭代后的w是 -5.614137,对应的loss值是 22.168112 第 14 次迭代后的w是 3.521854,对应的loss值是 21.290257 第 15 次迭代后的w是 -5.431417,对应的loss值是 20.447166 第 16 次迭代后的w是 3.342790,对应的loss值是 19.637461 第 17 次迭代后的w是 -5.255934,对应的loss值是 18.859821 第 18 次迭代后的w是 3.170815,对应的loss值是 18.112972 第 19 次迭代后的w是 -5.087399,对应的loss值是 17.395702 第 20 次迭代后的w是 3.005651,对应的loss值是 16.706835
我们发现如果学习率给的过大,导致无法收敛,学习没有效果。
使用指数衰减学习率
那么在梯度下降的过程中,学习率设置多少合适呢?在实际应用中,可以先用较大的学习率,快速找到最优值,然后逐步减小学习率,使模型在训练后期稳定,我们可以使用指数衰减学习率来达到这种效果。

上述公式的意义是,根据当前迭代次数,动态改变学习率的值,我们使用指数衰减学习率来根据学习的轮数,动态调整学习率,刚开始我们设定学习率等于 0.99,在每轮学习后,学习率都会调整,我们训练 20 轮就使得 loss 值为接近于零。
import tensorflow as tf epoch = 20 LR_BASE = 0.2 LR_DECAY = 0.99 LR_STEP = 1 w = tf.Variable(tf.constant(5, dtype=tf.float32)) # 我们给w随机初始化一个值5.0 for step in range(epoch): lr = LR_BASE * LR_DECAY ** (step / LR_STEP) with tf.GradientTape() as tape: loss = tf.square(w + 1) grads = tape.gradient(loss, w) w.assign_sub(lr * grads) print("第 %s 次迭代后的w是 %f,对应的loss值是 %f,学习率是%f" % (step + 1, w.numpy(), loss, lr))
程序运行结果如下:
第 1 次迭代后的w是 2.600000,对应的loss值是 36.000000,学习率是0.200000 第 2 次迭代后的w是 1.174400,对应的loss值是 12.959999,学习率是0.198000 第 3 次迭代后的w是 0.321948,对应的loss值是 4.728015,学习率是0.196020 第 4 次迭代后的w是 -0.191126,对应的loss值是 1.747547,学习率是0.194060 第 5 次迭代后的w是 -0.501926,对应的loss值是 0.654277,学习率是0.192119 第 6 次迭代后的w是 -0.691392,对应的loss值是 0.248077,学习率是0.190198 第 7 次迭代后的w是 -0.807611,对应的loss值是 0.095239,学习率是0.188296 第 8 次迭代后的w是 -0.879339,对应的loss值是 0.037014,学习率是0.186413 第 9 次迭代后的w是 -0.923874,对应的loss值是 0.014559,学习率是0.184549 第 10 次迭代后的w是 -0.951691,对应的loss值是 0.005795,学习率是0.182703 第 11 次迭代后的w是 -0.969167,对应的loss值是 0.002334,学习率是0.180876 第 12 次迭代后的w是 -0.980209,对应的loss值是 0.000951,学习率是0.179068 第 13 次迭代后的w是 -0.987226,对应的loss值是 0.000392,学习率是0.177277 第 14 次迭代后的w是 -0.991710,对应的loss值是 0.000163,学习率是0.175504 第 15 次迭代后的w是 -0.994591,对应的loss值是 0.000069,学习率是0.173749 第 16 次迭代后的w是 -0.996452,对应的loss值是 0.000029,学习率是0.172012 第 17 次迭代后的w是 -0.997660,对应的loss值是 0.000013,学习率是0.170292 第 18 次迭代后的w是 -0.998449,对应的loss值是 0.000005,学习率是0.168589 第 19 次迭代后的w是 -0.998967,对应的loss值是 0.000002,学习率是0.166903 第 20 次迭代后的w是 -0.999308,对应的loss值是 0.000001,学习率是0.165234
本节重要知识点
了解学习率的重要性。
会使用指数衰减学习率。




请登录后评论

