



自定义损失函数
阅读:1334201371 分享到损失函数是前向传播计算出的结果(预测值 y)与已知答案(标签 y_)的差距,神经网络的优化目标就是找到参与计算的参数(w 和 b),使得计算出来的预测值y和已知答案y_无限接近,也就是让他们的差距损失函数 loss 的值最小。
常用的损失函数
主流的损失函数loss有三种计算方法:均方误差,自定义,交叉熵。

在前面的学习中,我们一直在使用均方误差的方法,均方误差是前向传播计算出的结果 y 和已知答案 y_ 之差的平方再求平均,tf 提供函数 reduce_mean(tf.square(y-y_)) 来实现均方误差的计算。

一个案例
但是,根据现实情况,使用均方误差求损失函数并不能契合我们的需求,在此我们来看一个案例:预测酸奶预销量。
我们在酸奶销售过程中发现,每日的销售量和天气温度以及每日播放的酸奶广告有关,我们把天气温度和广告播放用 x1 和 x2 来表示,销量用 y_表示。也就是说 x1 和 x2 是特征值,y_ 是标签。
首先我们需要采集的数据有:每日的 x1 因素,x2 因素和当天的销量 y_ 作为我们的数据集,数据集越多效果越好。我们想要达到的目的是预测出每日生产多少酸奶最合适,毋庸置疑,产量等于销量是最合适的。
假定销量和特征值 x1,x2 之间的关系为:y_ = x1 + x2,我们根据这种假定的关系造一批数据集开始训练神经网络,最后用得出的模型根据 x1 和 x2 进行预测酸奶当日生产多少合适。
代码如下所示:
import tensorflow as tf import numpy as np epoch = 20000 # 训练20000次 Xcount = 32 # 样本个数 lr = 0.002 # 学习率 SEED = 22 # 随机种子 rdm = np.random.RandomState(seed=SEED) # 定义可以生成[0, 1)之间的随机数的对象 x = rdm.rand(Xcount, 2) # 生成300个特征值(x1,x2),这些值的范围为[0, 1) noise = (rdm.rand() / 10.0 - 0.05) # 生成(-0.5,0.5)之间的值作为噪音 y_ = [[x1 + x2 + noise] for (x1, x2) in x] # 生成标签 x = tf.cast(x, dtype=tf.float32) w1 = tf.Variable(tf.random.normal([2, 1], stddev=1, seed=1)) # 我们使用1层神经网络 for epoch in range(epoch): with tf.GradientTape() as tape: y = tf.matmul(x, w1) loss = tf.reduce_mean(tf.square(y_ - y)) # 均方误差作为损失函数 grads = tape.gradient(loss, w1) w1.assign_sub(lr * grads) if epoch % 2000 == 0: print("训练%d次后,w1的值为:\n%s" % (epoch, w1.numpy())) print("最终得到w1的值为:\n", w1.numpy())
程序运行的结果如下:
训练0次后,w1的值为: [[-0.80951774] [ 1.4857804 ]] 训练2000次后,w1的值为: [[0.345555] [1.670912]] 训练4000次后,w1的值为: [[0.6366915] [1.3994138]] 训练6000次后,w1的值为: [[0.7996717] [1.2385472]] 训练8000次后,w1的值为: [[0.89340925] [1.1459143 ]] 训练10000次后,w1的值为: [[0.9473535] [1.0926039]] 训练12000次后,w1的值为: [[0.97839797] [1.0619243 ]] 训练14000次后,w1的值为: [[0.99626356] [1.0442686 ]] 训练16000次后,w1的值为: [[1.0065433] [1.0341104]] 训练18000次后,w1的值为: [[1.0124593] [1.0282639]] 最终得到w1的值为: [[1.0158603] [1.0249006]]
由以上结果可知,使用均方误差的方式求损失函数 loss,经过 20000 次训练,w1 矩阵的值为 [[1.0158603], [1.0249006]],而且从规律上看,随着训练次数的增加 w1 的值逐渐趋向于矩阵 [[1], [1]],特征矩阵 x 和 w 的叉乘结果为预测值:y=1.0158603x1 + 1.0249006x2,这和我们的假定的函数 y = x1 + x2 非常符合。
上例中我们使用了 1 层神经网络,并且没有设置偏置项 b,因为我们预先知道这个神经网络的结构为:y = x1 + x2,也就是:y = [[1], [1]] 叉乘 [[x1, x2]] + 0,所以我们使用了 1 层神经网络也就是一个 w,并且设置了 b = 0。
我们也没有像前面的案例那样,对样本划分为 batch(因为我们的样本数比较少,一次性喂入神经网络是可以接受的),当然同学们可以生成更多一些的样本,然后使用 batch 来分批喂入神经网络做训练;我们也没有使用独热码,因为这不是个分类问题。
自己定义一个损失函数
我们在本例中使用均方误差作为损失函数,默认认为销量预测的多了或者少了,企业受到的损失是一样的,然而真实情况确是预测多了损失的是成本,预测少了损失的是利润,而利润和成本往往不想等,在这种现实情况下,使用均方误差计算 loss 是没办法让利益达到最大化的。
在此我们需要修改损失函数,根据本案例情况,我们先写出预测酸奶多或者少导致的损失 f(y_,y)。如果预测少了,损失值是每个酸奶的利润乘以少预测的酸奶数;如果预测多了损失值是每个酸奶的成本乘以多预测的酸奶的个数。
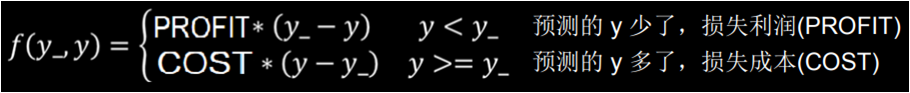
所以我们的自定义损失函数的公式为预测多或者少导致的损失的总和。

在代码中,我们可以写成如下形式。

如:预测酸奶销量,酸奶成本(COST)1 元,酸奶利润(PROFIT)99 元。预测少了损失利润 99 元,预测多了损失成本 1 元。预测少了损失大,我们希望训练出的神经网络模型往多了预测。
修改损失函数后的代码和运行结果如下。从结果上看,使用我们自定义损失函数训练得到的 w 矩阵的值大于 1,也就是我们模型倾向于往生产多了预测,这完全符合企业的利益。
import tensorflow as tf import numpy as np epoch = 20000 # 训练20000次 Xcount = 32 # 样本个数 lr = 0.002 # 学习率 SEED = 23455 # 随机种子 COST = 1 # 酸奶成本为1元 PROFIT = 9 # 酸奶利润为9元 rdm = np.random.RandomState(seed=SEED) # 定义可以生成[0, 1)之间的随机数的对象 x = rdm.rand(Xcount, 2) # 生成32个特征值(x1,x2),这些值的范围为[0, 1) noise = (rdm.rand() / 10.0 - 0.05) # 生成(-0.05,0.05)之间的值作为噪音 y_ = [[x1 + x2] for (x1, x2) in x] # 生成标签 x = tf.cast(x, dtype=tf.float32) w1 = tf.Variable(tf.random.normal([2, 1], stddev=1, seed=1)) # 我们使用1层神经网络 for epoch in range(epoch): with tf.GradientTape() as tape: y = tf.matmul(x, w1) loss = tf.reduce_sum(tf.where(tf.greater(y, y_), # 自定义损失函数 (y - y_) * COST, (y_ - y) * PROFIT)) grads = tape.gradient(loss, w1) w1.assign_sub(lr * grads) if epoch % 2000 == 0: print("训练%d次后,w1的值为:\n%s" % (epoch, w1.numpy())) print("最终得到w1的值为:\n", w1.numpy())
程序运行的结果如下:
训练0次后,w1的值为: [[-0.5490502] [ 1.6916239]] 训练2000次后,w1的值为: [[1.1933308] [1.2212298]] 训练4000次后,w1的值为: [[1.1934261] [1.2212775]] 训练6000次后,w1的值为: [[1.1935215] [1.2213252]] 训练8000次后,w1的值为: [[1.1936169] [1.2213728]] 训练10000次后,w1的值为: [[1.1937122] [1.2214205]] 训练12000次后,w1的值为: [[1.1938076] [1.2214682]] 训练14000次后,w1的值为: [[1.193903 ] [1.2215159]] 训练16000次后,w1的值为: [[1.1939983] [1.2215636]] 训练18000次后,w1的值为: [[1.1940937] [1.2216113]] 最终得到w1的值为: [[1.2246591] [1.2541895]]
现在我们修改成本为 99 元,利润为 1 元,大家试验一下训练出的模型是不是往少了预测。
交叉熵
还有另一种损失函数叫交叉熵,交叉熵损失函数 CE (Cross Entropy):表征两个概率分布之间的距离。交叉熵越大,两个概率分布越远;交叉熵越小,两个概率分布越近。交叉熵的计算公式如下:
其中 y_ 表示标准答案(标签)的概率分布,y 表示预测结果的概率分布。通过上述公式计算出交叉熵的值可以判断哪个预测结果与标准答案更接近。
我们举个例子来说明交叉熵的计算过程以及交叉熵是什么。比如:一个二分类案例中,已知标准答案y_ = (1, 0) ,我们用神经网络预测的一组概率 y1 = (0.6, 0.4) 和一组概率 y2 = (0.8, 0.2) ,这两个预测结果哪个更接近标准答案?直觉告诉我们,第二个更接近标准答案。我们使用交叉熵公式计算的结果如下。

从结果上我们可以看出,y1 和标准答案 y_ 的距离是 0.511;y2 与标准答案之间的距离为 0.223,因为 H1 > H2,所以 y2 预测更准,这个公式计算的结果符合我们的直觉。
Tensorflow 给出了交叉熵的计算公式:
tf.losses.categorical_crossentropy(y_, y)
我们用代码验证该公式的效果。
import tensorflow as tf loss_ce1 = tf.losses.categorical_crossentropy([1.0, 0], [0.6, 0.4]) loss_ce2 = tf.losses.categorical_crossentropy([1.0, 0], [0.8, 0.2]) print("loss_ce1:", loss_ce1) print("loss_ce2:", loss_ce2)
代码运行的结果如下,我们发现结果和公式计算结果一致。
loss_ce1: tf.Tensor(0.5108256, shape=(), dtype=float32) loss_ce2: tf.Tensor(0.22314353, shape=(), dtype=float32)
我们在执行分类问题时,通常先用 softmax 函数让输出结果符合概率分布,再计算 y_ 与 y 之间的交叉熵损失函数,tf 给出了一个可以同时计算概率分布和交叉熵的函数:
Tf.nn.softmax_cross_entropy_with_logits(y_, y)
import tensorflow as tf import numpy as np y_ = np.array([[1, 0, 0], [0, 1, 0], [0, 0, 1], [1, 0, 0], [0, 1, 0]]) y = np.array([[12, 3, 2], [3, 10, 1], [1, 2, 5], [4, 6.5, 1.2], [3, 6, 1]]) y_pro = tf.nn.softmax(y) loss_ce1 = tf.losses.categorical_crossentropy(y_, y_pro) loss_ce2 = tf.nn.softmax_cross_entropy_with_logits(y_, y) print("使用两个公式计算的结果:", loss_ce1) print("使用综合公式计算的结果:", loss_ce2)
代码运行的结果如下:
使用两个公式计算的结果: tf.Tensor([1.68795487e-04 1.03475622e-03 6.58839038e-02 2.58349207e+00 5.49852354e-02], shape=(5,), dtype=float64) 使用综合公式计算的结果: tf.Tensor([1.68795487e-04 1.03475622e-03 6.58839038e-02 2.58349207e+00 5.49852354e-02], shape=(5,), dtype=float64)
本节重要知识点
了解常用的损失函数。
根据业务场景会自定义损失函数。
掌握交叉熵。





