



神经网络具体实现
阅读:1316940923 分享到我们已经了解了神经网络搭建的流程并学习了 tf 提供的一些常用函数,本节课我们开始用 tf 搭建一个可以实现识别鸢尾花的神经网络模型来变现我们所学的知识。
鸢尾花数据集
搭建识别鸢尾花的神经网络首先我们需要鸢尾花数据集,相关研究人员已经收集好了足够数量的鸢尾花数据集。这些鸢尾花数据集共有 150 组,每组包括鸢尾花的花萼 长、花萼宽、花瓣长、花瓣宽 4 个输入特征,同时还给出了这一组特征对应的 鸢尾花类别。类别包括狗尾鸢尾、杂色鸢尾、弗吉尼亚鸢尾三类,分别用数字 0、1、2 表示。

我们可以通过 skearn 包中的 datasets 直接下载数据集,代码如下。
from sklearn.datasets import load_iris x_data = load_iris().data # 返回iris数据集所有输入特征值 y_data = load_iris().target # 返回iris数据集所有标签
其中 load_iris().data 返回鸢尾花数据集里面的所有输入特征,相关人员已经把各种种类的鸢尾花图片给量化成了相对应的特征值;load_iris().target 返回鸢尾花数据集中的特征值对应的标签,这些标签表示该特征值对应的是哪一种类的鸢尾花。
我们打印出数据集的特征值和标签,先看一下这些数据的特点。
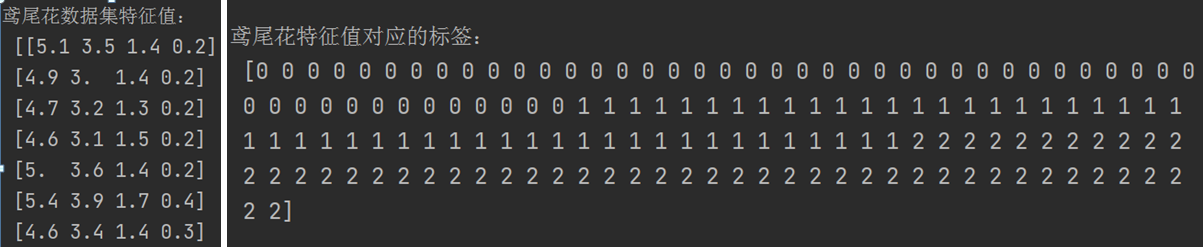
from sklearn.datasets import load_iris x_data = load_iris().data # 返回iris数据集所有输入特征值 y_data = load_iris().target # 返回iris数据集所有标签 print("鸢尾花数据集特征值:\n", x_data) print("鸢尾花特征值对应的标签:\n", y_data)
下面截图是打印出的鸢尾花特征值(部分)和标签。
为了更友好的显示这些数据,我们给给数据集添加索引,然后把标签合并到数据集中一块显示出来。
from sklearn.datasets import load_iris from pandas import DataFrame import pandas as pd x_data = load_iris().data # 返回iris数据集所有输入特征值 y_data = load_iris().target # 返回iris数据集所有标签 x_data = DataFrame(x_data, columns=["花萼长", "花萼宽", "花瓣长", "花瓣宽"]) pd.set_option("display.unicode.east_asian_width", True) # 设置列名对齐 print("给数据集添加索引: \n", x_data) x_data["类别"] = y_data # 新加一列,列标签为“类别”,数据为y_data print("给数据集加上一列标签:\n", x_data)
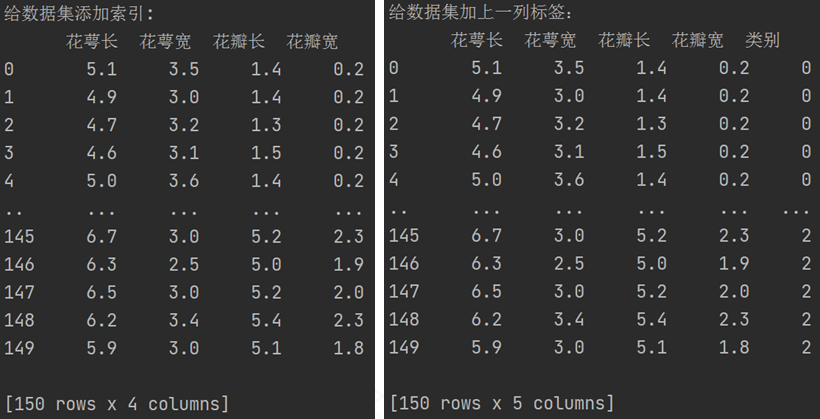
这样我们就能更清晰的看到数据集的特征值和标签之间的一一对应关系了。
数据集预处理
人类在认识这个世界的时候,信息是没有规律的,比如我们小时候认识鸡鸭鹅的时候,不可能先学会认识一定数量的鸡,然后再学会认识一定数量的鸭等等,我们一般是鸡鸭鹅这些家禽同时杂乱无章的涌入我们的大脑,我们的神经网络是同时学会认识这些家禽的。
前面我们已经看到我们的 150 条鸢尾花数据集是按照 0 类、1 类、2 类顺序排列的,我们如果想让我们的神经网络更好的学习这些识别鸢尾花的知识,首先我们要先打乱这些数据集,然后再让我们的神经网络去学习,这样更接近现实世界的学习情况。
from sklearn.datasets import load_iris import numpy as np from pandas import DataFrame import pandas as pd x_data = load_iris().data # 返回iris数据集所有输入特征值 y_data = load_iris().target # 返回iris数据集所有标签 # 因为 x_data 和 y_data 使用同样的随机种子,打乱顺序的算法是一样的,所以打乱后的特征和标签对应关系保持不变 np.random.seed(1024) # 设置随机种子 np.random.shuffle(x_data) # 按随机种子打乱数据顺序 np.random.seed(1024) # 设置随机种子 np.random.shuffle(y_data) # 按随机种子打乱数据顺序 x_data = DataFrame(x_data, columns=["花萼长", "花萼宽", "花瓣长", "花瓣宽"]) pd.set_option("display.unicode.east_asian_width", True) # 设置列名对齐 x_data["类别"] = y_data # 新加一列,列标签为“类别”,数据为y_data print("给数据集加上一列标签:\n", x_data)
因为 x_data 和 y_data 使用同样的随机种子,打乱顺序的算法是一样的,所以打乱后的特征和标签对应关系保持不变,程序运行的结果如下:
给数据集加上一列标签: 花萼长 花萼宽 花瓣长 花瓣宽 类别 0 5.0 2.3 3.3 1.0 1 1 4.8 3.4 1.9 0.2 0 2 7.6 3.0 6.6 2.1 2 3 5.7 2.5 5.0 2.0 2 4 4.7 3.2 1.6 0.2 0 .. ... ... ... ... ... 145 6.2 3.4 5.4 2.3 2 146 5.5 2.5 4.0 1.3 1 147 5.8 2.7 5.1 1.9 2 148 6.2 2.9 4.3 1.3 1 149 6.7 3.0 5.2 2.3 2 [150 rows x 5 columns]
我们把打乱后的数据集中前 120 个数据取出来作为训练集,后 30 个数据作为测试集,为了公正判断神经网络的效果,训练集和测试集要求是没有交集的。
# 取前120条数据集作为训练集 x_train = x_data[:-30] y_train = y_data[:-30] # 取后30条数据集作为测试集 x_test = x_data[-30:] y_test = y_data[-30:]
我们获取的数据集(特征和标签)是 numpy 类型的,在后面计算中我们需要让特征和 w 矩阵做叉乘,而w矩阵我们定义为 tensor 类型的,在此我们需要使用 cast 函数把需要计算的特征值(训练集中的特征和测试集中的特征)转为 tensor 类型的数据。
# 转变特征的数据类型(把numpy类型的数据转为Tensor类型的数据),否则后面矩阵叉乘时会因为数据类型不一致报语法错误 x_train = tf.cast(x_train, tf.float32) x_test = tf.cast(x_test, tf.float32)
使用 from_tensor_slices 把训练集的输入特征和标签配对打包,每 32 组输入特征和标签对打包为一个 batch,我们会以 batch 为单位一批一批的喂入神经网络,这个就如我们学习一样,要一部分一部分的学习,而不是一个口吃个大胖子。
# 配对特征和标签,每次喂入神经网络一个batch train_db = tf.data.Dataset.from_tensor_slices((x_train, y_train)).batch(32) test_db = tf.data.Dataset.from_tensor_slices((x_test, y_test)).batch(32)
然后我们开始初始化 w 和 b,刚开始的 w 和 b 我们给个随机值,然后用数据集开始训练神经网络,让神经网络不停的纠错学习,最终得到最优的 w 和 b,w 和 b 即是我们训练好的神经网络模型。
# 定义神经网络中所有可训练参数 w1 = tf.Variable(tf.random.truncated_normal([4, 3], stddev=0.1, seed=1)) b1 = tf.Variable(tf.random.truncated_normal([3], stddev=0.1, seed=1))
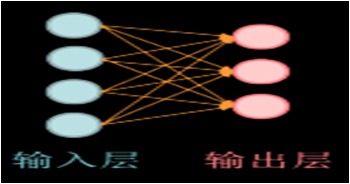
根据公式:y = x叉乘w + b,因为输入特征 x 是 120 行 4 列,为了支持矩阵叉乘,所以 w 的行必须是 4,因为输出标签y是 3 列的,所以w的列必须是 3;为了支持矩阵加法,b1 必须与 w1 的列一致,所以 b1 向量的元素个数为 3。到这里我们的神经网络结构已经搭建出来了。
注意,我们目前使用的神经网络只有一层,所以我们只需要一个w,当然我们也可以搭建2层或者多层的神经网络。
训练神经网络
接下来我们开始写代码让神经网络开始根据数据集学习,并不停的减少损失函数来更新参数 w 和 b,我们让损失函数值尽量越来越小,对 w 和 b 的优化就会越来越精确,训练出来的神经网络对鸢尾花识别的准确度就会越来越高。
''' 这个for迭代500次,每次学习一个batch组数据集(第1组batch:32个数据集;第2组 第2组batch:32个数据集;第3组batch:32个数据集;第4组batch:24个数据集) ''' for epoch in range(epoch): # 下面的for迭代4次(train_db有4个元素,每个元素是一个batch) for step, (x_train, y_train) in enumerate(train_db): with tf.GradientTape() as tape: y = tf.matmul(x_train, w1) + b1 # 神经网络模型 y = tf.nn.softmax(y) # 使y符合概率分布并可以和独热码对比 y_ = tf.one_hot(y_train, depth=3) # 将标签转换为独热码(3分类) loss = tf.losses.categorical_crossentropy(y_, y) # loss = tf.reduce_mean(tf.square(y_ - y)) # 损失函数 grads = tape.gradient(loss, [w1, b1]) # 让loss分别对w1和b1求偏导 w1.assign_sub(lr * grads[0]) # 更新w1(w1 = w1 - lr * w1_grad) b1.assign_sub((lr * grads[1])) # 更新b1(b1 = b1 - lr * b1_grad) print("轮数:%s,loss值:%f" % (epoch, loss))
现在我们已经构建了完整的可以识别鸢尾花的神经网络,完整代码如下:
import tensorflow as tf from sklearn.datasets import load_iris import numpy as np x_data = load_iris().data # 返回iris数据集所有输入特征值 y_data = load_iris().target # 返回iris数据集所有标签 # 因为x_data和y_data使用同样的随机种子,打乱顺序的算法是一样的,所以打乱后的特征和标签对应关系保持不变 np.random.seed(1024) # 设置随机种子 np.random.shuffle(x_data) # 按随机种子打乱数据顺序 np.random.seed(1024) # 设置随机种子 np.random.shuffle(y_data) # 按随机种子打乱数据顺序 # 取前120条数据集作为训练集 x_train = x_data[:-30] y_train = y_data[:-30] # 取后30条数据集作为测试集 x_test = x_data[-30:] y_test = y_data[-30:] # 转变特征的数据类型(把numpy类型的数据转为Tensor类型的数据),否则后面矩阵叉乘时会因为数据类型不一致报语法错误 x_train = tf.cast(x_train, tf.float32) x_test = tf.cast(x_test, tf.float32) # 配对特征和标签,每次喂入神经网络一个batch train_db = tf.data.Dataset.from_tensor_slices((x_train, y_train)).batch(32) test_db = tf.data.Dataset.from_tensor_slices((x_test, y_test)).batch(32) # 定义神经网络中所有可训练参数 w1 = tf.Variable(tf.random.truncated_normal([4, 3], stddev=0.1, seed=1)) b1 = tf.Variable(tf.random.truncated_normal([3], stddev=0.1, seed=1)) # epoch = 500 # 循环学习500次,看实际情况,如果学习的知识太复杂可以增加学习轮数 lr = 0.2 # 定义学习率,也可以根据实际情况调整 ''' 这个for迭代500次,每次学习一个batch组数据集(第1组batch:32个数据集;第2组 第2组batch:32个数据集;第3组batch:32个数据集;第4组batch:24个数据集) ''' for epoch in range(epoch): # 下面的for迭代4次(train_db有4个元素,每个元素是一个batch) for step, (x_train, y_train) in enumerate(train_db): with tf.GradientTape() as tape: y = tf.matmul(x_train, w1) + b1 # 神经网络模型 y = tf.nn.softmax(y) # 使y符合概率分布并可以和独热码对比 y_ = tf.one_hot(y_train, depth=3) # 将标签转换为独热码(3 分类) loss = tf.reduce_mean(tf.square(y_ - y)) # 损失函数 grads = tape.gradient(loss, [w1, b1]) # 让loss分别对w1和b1求偏导 w1.assign_sub(lr * grads[0]) # 更新w1(w1 = w1 - lr * w1_grad) b1.assign_sub((lr * grads[1])) # 更新b1(b1 = b1 - lr * b1_grad) print("轮数:%s,loss值:%f" % (epoch, loss)) # 打印出训练完成后的 w1 和 b1 的值 print(w1, b1)
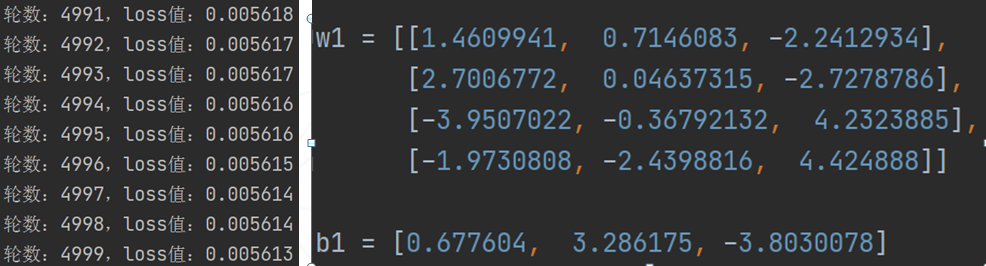
我们训练 5000 轮后,loss 的值等于 0.005613,这个值已经很小了,记住,由于 loss 函数的复杂性,我们不一定容易找到最小值,也没有必要一定要找到最小值,最后我们打印出训练 5000 轮后得到的 w1 和 b1 的值。结果如下图所示(打印轮数为部分截图):
预测结果
我们使用训练 5000 轮后得到的 w1 和 b1 的值,然后把测试集中的特征作为 x 带入公式:y = x叉乘w1 + b1 得到 y 的值,我们得到的 y 值和测试集中的标签对比,看看对 30 个鸢尾花的预测的正确性如何。
# 划分不相交的训练集和测试集 import tensorflow as tf from sklearn.datasets import load_iris import numpy as np x_data = load_iris().data # 返回iris数据集所有输入特征值 y_data = load_iris().target # 返回iris数据集所有标签 # 因为x_data和y_data使用同样的随机种子,打乱顺序的算法是一样的,所以打乱后的特征和标签对应关系保持不变 np.random.seed(1024) # 设置随机种子 np.random.shuffle(x_data) # 按随机种子打乱数据顺序 np.random.seed(1024) # 设置随机种子 np.random.shuffle(y_data) # 按随机种子打乱数据顺序 # 取前120条数据集作为训练集 x_train = x_data[:-30] y_train = y_data[:-30] # 取后30条数据集作为测试集 x_test = x_data[-30:] y_test = y_data[-30:] # 转变特征的数据类型(把numpy类型的数据转为Tensor类型的数据),否则后面矩阵叉乘时会因为数据类型不一致报语法错误 x_train = tf.cast(x_train, tf.float32) x_test = tf.cast(x_test, tf.float32) # 配对特征和标签,每次喂入神经网络一个 batch train_db = tf.data.Dataset.from_tensor_slices((x_train, y_train)).batch(32) test_db = tf.data.Dataset.from_tensor_slices((x_test, y_test)).batch(32) # 训练后得出的 w1 和 b1 的值 w1 = [[1.4609941, 0.7146083, -2.2412934], [2.7006772, 0.04637315, -2.7278786], [-3.9507022, -0.36792132, 4.2323885], [-1.9730808, -2.4398816, 4.424888]] b1 = [0.677604, 3.286175, -3.8030078] # 使用神经网络模型 w1 和 b1 去识别鸢尾花种类 for x_test, y_test in test_db: # 一次性喂入30个数据集的特征到神经网络 y = tf.matmul(x_test, w1) + b1 # 用求出的w1和b1根据测试集中的特征预测结果 y = tf.nn.softmax(y) # 让y符合概率分布 pred = tf.argmax(y, axis=1) # 返回y中最大值的索引,既预测的分类 print(pred) # 每个特征值预测的结果 print(y_test) # 测试集中的每个特征对应的标签,测试集中的30个标签
程序运行结果如下图,我们发现除了第一个预测错误,其余都预测正确。
tf.Tensor([2 2 0 1 0 1 1 2 0 0 0 0 0 2 0 1 1 0 1 0 0 1 1 0 1 2 1 2 1 2], shape=(30,), dtype=int64) tf.Tensor([1 2 0 1 0 1 1 2 0 0 0 0 0 2 0 1 1 0 1 0 0 1 1 0 1 2 1 2 1 2], shape=(30,), dtype=int32)
当然,我们也可以使用我们训练出来的模型(w1 和 b1)进行一个一个的预测,这个时候代码中的 test_db 的定义就需要改成每个特征值和标签作为一个 batch,如下面这样。
test_db = tf.data.Dataset.from_tensor_slices((x_test, y_test))
这样一来,test_db 中每个 batch 就是一个鸢尾花对应的特征值和标签的配对,这样的话它只是一个向量,所以在预测时,我们就需要把每个 x_test 改成矩阵。
# 使用神经网络模型 w1 和 b1 去识别鸢尾花种类 for x_test, y_test in test_db: # 一次性喂入1个数据集的特征到神经网络,共喂入30次 y = tf.matmul([x_test], w1) + b1 # 用求出的w1和b1根据测试集中的特征预测结果 y = tf.nn.softmax(y) # 让y符合概率分布 pred = tf.argmax(y, axis=1) # 返回y中最大值的索引,既预测的分类 print(pred) # 每个特征值预测的结果 print(y_test) # 测试集中的每个特征对应的标签,测试集中的30个标签
通过打印的结果,我们发现除了第一个预测错误,其它都预测成功。大家可以自行试验,我就不贴出来代码运行的结果了。
我们统计神经网络层数时,只统计具有运算能力的层,输入层只是把数据传输过来,并没有运算,所以在统计神经网络层数时不算输入层。
神经网络层数
我们统计神经网络层数时,只统计具有运算能力的层,输入层只是把数据传输过来,并没有运算,所以在统计神经网络层数时不算输入层。
输入层和输出层之间的所有层都叫做隐藏层,神经网络的层数是N个隐藏层的层数加上 1 个输出层。如下图神经网络输入层有 3 个节点(特征值);隐藏层只有 1 层,有 4 个节点;输出层有 2 个节点。该神经网络共有 2 层,第1层是 3 行 4 列的 w 加上 4 个偏置项 b,第二层是 4 行 2 列的 w 加上 2 个偏置项 b。
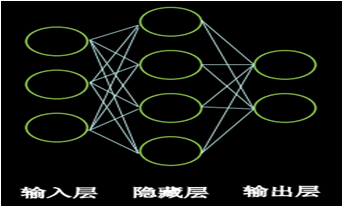
在本次识别鸢尾花案例中,我们使用了一层神经网络(只有计算输出层的一个 w,没有隐藏层),当然我们可以搭建 N 层神经网络结构( N 个 w),其实,通常情况下,我们一般使用两层神经网络结构,也就是说我们要初始化两个 w,面我们来使用两层神经网络结构来构建我们的神经网络。
注意为了此时的神经网络数学公式则为:y = ((x叉乘w1)+ b1)叉乘w2 + b2。为了支持矩阵叉乘,w1 矩阵的列要等于特征x矩阵的行,w2 矩阵的行要等于w1矩阵的列;w2 矩阵的列要等于 y 矩阵的列。我们已知 x 矩阵是 N 行 4 列,所以 w1 的行为 4,列可以自己设定,我们假定 w1 的列为 3,则 w2 的行也要等于 3,因为 y 是 3 分类,y 的列为 3,所以 w2 的列为 3。
所以代码中,在定义神经网络中的所有可训练参数中,我们需要添加一个 w2 和 b2。
# 定义神经网络中所有可训练参数 w1 = tf.Variable(tf.random.truncated_normal([4, 3], stddev=0.1, seed=1)) w2 = tf.Variable(tf.random.truncated_normal([3, 3], stddev=0.1, seed=1)) b1 = tf.Variable(tf.random.truncated_normal([3], stddev=0.1, seed=1)) b2 = tf.Variable(tf.random.truncated_normal([3], stddev=0.1, seed=1))
训练过程的代码,我们也要加入对 w1,w2 和 b1,b2 的调整,代码修改如下:
for epoch in range(epoch): # 下面的for迭代4次(train_db有4个元素,每个元素是一个batch) for step, (x_train, y_train) in enumerate(train_db): with tf.GradientTape() as tape: a = tf.matmul(x_train, w1) + b1 # 计算第 1 层神经网络模型 y = tf.matmul(a, w2) + b2 # 计算第 2 次神经网络模型 y = tf.nn.softmax(y) # 使y符合概率分布并可以和独热码对比 y_ = tf.one_hot(y_train, depth=3) # 将标签转换为独热码(3分类) loss = tf.reduce_mean(tf.square(y_ - y)) # 损失函数 grads = tape.gradient(loss, [w1, w2, b1, b2]) # 让loss分别对w1,w2和b1,b2求偏导 w1.assign_sub(lr * grads[0]) # 更新w1(w1 = w1 - lr * w1_grad) w2.assign_sub(lr * grads[1]) # 更新w2(w2 = w2 - lr * w2_grad) b1.assign_sub((lr * grads[2])) # 更新b1(b1 = b1 - lr * b1_grad) b2.assign_sub((lr * grads[3])) # 更新b2(b2 = b2 - lr * b2_grad) print("轮数:%s,loss值:%f" % (epoch, loss)) # 打印出训练完成后的 w1,w2 和 b1,b2 的值 print(w1, w2, b1, b2)
构建训练两层神经网络的完整代码如下:
import tensorflow as tf from sklearn.datasets import load_iris import numpy as np x_data = load_iris().data # 返回iris数据集所有输入特征值 y_data = load_iris().target # 返回iris数据集所有标签 # 因为x_data和y_data使用同样的随机种子,打乱顺序的算法是一样的,所以打乱后的特征和标签对应关系保持不变 np.random.seed(1024) # 设置随机种子 np.random.shuffle(x_data) # 按随机种子打乱数据顺序 np.random.seed(1024) # 设置随机种子 np.random.shuffle(y_data) # 按随机种子打乱数据顺序 # 取前120条数据集作为训练集 x_train = x_data[:-30] y_train = y_data[:-30] # 取后30条数据集作为测试集 x_test = x_data[-30:] y_test = y_data[-30:] # 转变特征的数据类型(把numpy类型的数据转为Tensor类型的数据),否则后面矩阵叉乘时会因为数据类型不一致报语法错误 x_train = tf.cast(x_train, tf.float32) x_test = tf.cast(x_test, tf.float32) # 配对特征和标签,每次喂入神经网络一个batch train_db = tf.data.Dataset.from_tensor_slices((x_train, y_train)).batch(32) test_db = tf.data.Dataset.from_tensor_slices((x_test, y_test)).batch(32) # 定义神经网络中所有可训练参数 w1 = tf.Variable(tf.random.truncated_normal([4, 3], stddev=0.1, seed=1)) w2 = tf.Variable(tf.random.truncated_normal([3, 3], stddev=0.1, seed=1)) b1 = tf.Variable(tf.random.truncated_normal([3], stddev=0.1, seed=1)) b2 = tf.Variable(tf.random.truncated_normal([3], stddev=0.1, seed=1)) epoch = 500 # 循环学习500次,看实际情况,如果学习的知识太复杂可以增加学习轮数 lr = 0.2 # 定义学习率,也可以根据实际情况调整 ''' 这个for迭代500次,每次学习一个batch组数据集(第1组batch:32个数据集;第2组 第2组batch:32个数据集;第3组batch:32个数据集;第4组batch:24个数据集) ''' for epoch in range(epoch): # 下面的for迭代4次(train_db有4个元素,每个元素是一个batch) for step, (x_train, y_train) in enumerate(train_db): with tf.GradientTape() as tape: a = tf.matmul(x_train, w1) + b1 # 计算第 1 层神经网络模型 y = tf.matmul(a, w2) + b2 # 计算第 2 次神经网络模型 y = tf.nn.softmax(y) # 使y符合概率分布并可以和独热码对比 y_ = tf.one_hot(y_train, depth=3) # 将标签转换为独热码(3分类) loss = tf.reduce_mean(tf.square(y_ - y)) # 损失函数 grads = tape.gradient(loss, [w1, w2, b1, b2]) # 让 loss 分别对 w1,w2 和 b1,b2 求偏导 w1.assign_sub(lr * grads[0]) # 更新w1(w1 = w1 - lr * w1_grad) w2.assign_sub(lr * grads[1]) # 更新w2(w2 = w2 - lr * w2_grad) b1.assign_sub((lr * grads[2])) # 更新b1(b1 = b1 - lr * b1_grad) b2.assign_sub((lr * grads[3])) # 更新b2(b2 = b2 - lr * b2_grad) print("轮数:%s,loss值:%f" % (epoch, loss)) # 打印出训练完成后的 w1,w2 和 b1,b2 的值 print(w1, w2, b1, b2)
通过训练,我们发现同样是训练 5000 轮,我们用 2 层神经网络得到的 loss 值要比用 1 层神经网络得到模型更精确(相对比损失值较小)。下图是损失值的变化(部分截图)和 w1,w2,b1,b2 的结果。
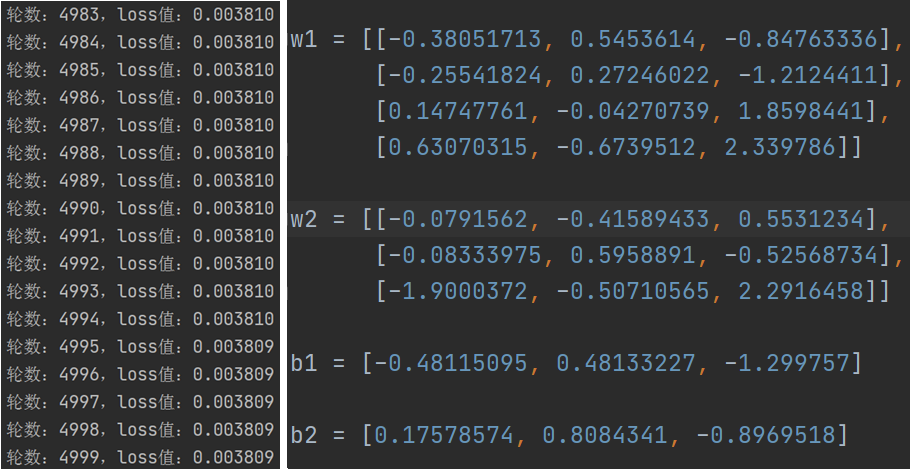
训练完成后,我们得到 w1,w2 和 b1,b2 的值,然后用这些值对测试集中的特征做预测,预测的代码修改如下:
# 使用神经网络模型 w1,w2 和 b1,b2 去识别鸢尾花种类 for x_test, y_test in test_db: # 一次性喂入30个数据集的特征到神经网络,共喂入 1 次 a = tf.matmul(x_test, w1) + b1 # 计算第 1 层神经网络 y = tf.matmul(a, w2) + b2 # 用求出预测结果y y = tf.nn.softmax(y) # 让 y 符合概率分布 pred = tf.argmax(y, axis=1) # 返回 y 中最大值的索引,既预测的分类 print(pred) # 每个特征值预测的结果 print(y_test) # 测试集中的每个特征对应的标签,测试集中的 30 个标签
使用两层神经网络模型(w1,w2 和 b1,b2)预测鸢尾花的完整代码如下:
import tensorflow as tf from sklearn.datasets import load_iris import numpy as np x_data = load_iris().data # 返回iris数据集所有输入特征值 y_data = load_iris().target # 返回iris数据集所有标签 # 因为x_data和y_data使用同样的随机种子,打乱顺序的算法是一样的,所以打乱后的特征和标签对应关系保持不变 np.random.seed(1024) # 设置随机种子 np.random.shuffle(x_data) # 按随机种子打乱数据顺序 np.random.seed(1024) # 设置随机种子 np.random.shuffle(y_data) # 按随机种子打乱数据顺序 # 取前120条数据集作为训练集 x_train = x_data[:-30] y_train = y_data[:-30] # 取后30条数据集作为测试集 x_test = x_data[-30:] y_test = y_data[-30:] # 转变特征的数据类型(把numpy类型的数据转为Tensor类型的数据),否则后面矩阵叉乘时会因为数据类型不一致报语法错误 x_train = tf.cast(x_train, tf.float32) x_test = tf.cast(x_test, tf.float32) # 配对特征和标签,每次喂入神经网络一个batch train_db = tf.data.Dataset.from_tensor_slices((x_train, y_train)).batch(32) test_db = tf.data.Dataset.from_tensor_slices((x_test, y_test)).batch(32) # 训练后得出的 w1 和 b1 的值 w1 = [[-0.38051713, 0.5453614, -0.84763336], [-0.25541824, 0.27246022, -1.2124411], [0.14747761, -0.04270739, 1.8598441], [0.63070315, -0.6739512, 2.339786]] w2 = [[-0.0791562, -0.41589433, 0.5531234], [-0.08333975, 0.5958891, -0.52568734], [-1.9000372, -0.50710565, 2.2916458]] b1 = [-0.48115095, 0.48133227, -1.299757] b2 = [0.17578574, 0.8084341, -0.8969518] # 使用神经网络模型 w1,w2 和 b1,b2 去识别鸢尾花种类 for x_test, y_test in test_db: # 一次性喂入30个数据集的特征到神经网络,共喂入1次 a = tf.matmul(x_test, w1) + b1 # 计算第 1 层神经网络 y = tf.matmul(a, w2) + b2 # 用求出预测结果y y = tf.nn.softmax(y) # 让y符合概率分布 pred = tf.argmax(y, axis=1) # 返回y中最大值的索引,既预测的分类 print(pred) # 每个特征值预测的结果 print(y_test) # 测试集中的每个特征对应的标签,测试集中的30个标签
程序运行后,我们发现除了第一个预测错误,其它完全正确。
tf.Tensor([2 2 0 1 0 1 1 2 0 0 0 0 0 2 0 1 1 0 1 0 0 1 1 0 1 2 1 2 1 2], shape=(30,), dtype=int64) tf.Tensor([1 2 0 1 0 1 1 2 0 0 0 0 0 2 0 1 1 0 1 0 0 1 1 0 1 2 1 2 1 2], shape=(30,), dtype=int32)
大家从本案例中可能看不出两层神经网络对预测结果有什么改善,但是从理论上来说神经网络的层数越多(类似人脑的神经元越多),就会越聪明,学习起来效果越好, 从训练的过程中的损失值的对比,我们也发现了在同等条件下(学习算法一样),确实两层神经网络比一层神经网络学习的效果好。
本节重要知识点
会使用数据集
编写神经网络训练代码
使用训练好的神经网络模型做预测





