Tensorflow常用函数介绍

Tensorflow 提供了大量的实用的函数，在此我们来介绍一下常用的函数，这些函数功能丰富，大家一定要学会使用它。下面为了方便讲解，我们称 Tensorflow 为 tf。

数据处理函数

tf 的 convert_to_tensor 函数可以将 numpy 的数据类型转为 tensor 数据类型。

import tensorflow as tf
import numpy as np

a = np.arange(0, 5)
b = tf.convert_to_tensor(a, dtype=tf.int32)

print(a)
print(b)

程序运行结果如下：

[0 1 2 3 4]
tf.Tensor([0 1 2 3 4], shape=(5,), dtype=int32)

tf 中的数据存储和处理的 API 大都和科学计算库中的 numpy，pandas 等类似而且内部 API 的实现也会直接使用这些库，下一章节，我们会重点介绍这些数据处理模块。在上面的 convert_to_tensor 我们给定两个参数（数据名， dtype=数据类型（可选））。

tf 的 zeros（维度）函数可以创建全为 0 的张量；tf 的 ones（维度）函数可以创建全为 1 的张量；tf 的 fill（维度，指定值）可以创建全为指定值的张量，下面我们看下这些函数的用法。

import tensorflow as tf

a = tf.zeros((2, 3))
b = tf.ones((6,))
c = tf.fill((3, 2), 8)

print(a)
print(b)
print(c)

程序运行结果如下：

tf.Tensor([[0. 0. 0.]
           [0. 0. 0.]], shape=(2, 3), dtype=float32)
tf.Tensor([1. 1. 1. 1. 1. 1.], shape=(6,), dtype=float32)
tf.Tensor([[8 8]
           [8 8]
           [8 8]], shape=(3, 2), dtype=int32)

注意：要记住维度的写法：一维直接写个数；二维用 [行, 列], 多维用 [n,m,j,k…] 的方式。大家可以试着使用以上函数生成你需要的张量数据。

在使用 tf 中，我们常常使用随机生成的初始化参数，有时候我们需要指定这些随机数据符合什么类型的分布更符合我们需求，常用的数据分布有正态分布，均匀分布等，tf 提供了生成符合各种分布的随机数据的 API。

tf 的 random.normal(维度，mean=均值，stddev=标准差）函数可以生成符合正态分布的随机数，默认均值为 0，标准差为 1。

import tensorflow as tf

d = tf.random.normal([3, 2], mean=0.5, stddev=1)

print(d)

程序运行结果如下：

tf.Tensor(
[[ 0.12048551  0.07763442]
[-0.45974946 -0.48435694]
[-0.09332967  0.30089152]], shape=(3, 2), dtype=float32)

如上代码，我们生成 3 行 2 列的符合正态分布的随机数，里面的数据符合以 0.5 为均值，1 为标准差的分布。

有时候我们想让生成的符合正态分布的随机数更集中一些，也就是生成截断式正态分布的随机数，我们可以使用 tf 的 random.truncated_normal(维度，mean=均值，stddev=标准差）函数，这个函数可以保证生成的随机数在（μ-2σ，μ+2σ）之内，对于随机数落在这个范围之外的则会重新进行生成，该函数保证了生成的随机数据在均值附近。

import tensorflow as tf

e = tf.random.truncated_normal([3, 2], mean=0.5, stddev=1)

print(e)

程序运行结果如下：

tf.Tensor(
[[ 1.428692    1.1968148 ]
[ 2.0154333  -0.25715703]
[ 1.506125   -0.0620895 ]], shape=(3, 2), dtype=float32)

我们发现这些随机数据都在两倍标准差之内，数据更向均值 0.5 集中

tf 的 uniform（维度，minval=最小值，maxval=最大值）函数可以生成在最小值和最大值之间的符合均匀分布的随机数。

import tensorflow as tf

f = tf.random.uniform([3, 2], minval=-2, maxval=3)

print(f)

程序运行结果如下：

tf.Tensor(
[[-0.5175055  2.895114 ]
[-1.318676   2.8742094]
[ 1.0499082 -1.9198747]], shape=(3, 2), dtype=float32)

注意生成的随机数落在最小值和最大值的区间是左闭右开 [minval, maxval)，也就是这些随机数 >= minval 且 这些随机数 < maxval。

数据计算函数

tf 的 cast（张量名，dtype=数据类型）函数可以强制 tensor 转为该数据类型。下面代码中我们定义一个向量 x1，里面的数据都是整数类型，然后我们使用 cast 函数转为浮点数类型。

import tensorflow as tf

x1 = tf.constant([1, 2, 3], dtype=tf.int64)
x2 = tf.cast(x1, dtype=tf.float64)

print(x1)
print(x2)

程序运行结果如下：

tf.Tensor([1 2 3], shape=(3,), dtype=int64)
tf.Tensor([1. 2. 3.], shape=(3,), dtype=float64)

tf 的 reduce_min(张量名），可以计算张量元素的最小值；tf 的 reduce_max 函数可以计算张量元素的最大值；以上两个函数返回计算后的元素值。

import tensorflow as tf

x1 = tf.constant([1, 2, 3], dtype=tf.int64)

print(tf.reduce_min(x1))
print(tf.reduce_max(x1))

程序运行结果如下：

tf.Tensor(1, shape=(), dtype=int64)
tf.Tensor(3, shape=(), dtype=int64)

tf 的 axis 参数可以指定操作的方向，例如：在一个二维张量或数组中，如果 axis=0，表示对第一个维度进行操作，axis=1 表示对第二个维度进行操作，计算的结果的维度是原来数据的维度减一。

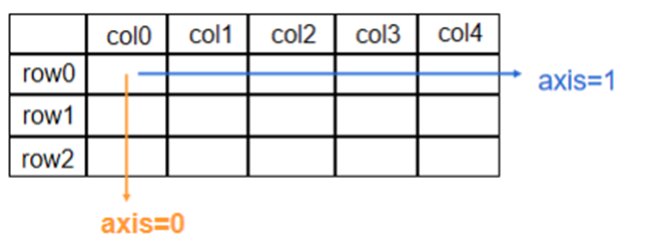
下面我们定义一个二维矩阵，然后使用 axis 参数来指定求和的方向，我们可以使用 axis=0 让 reduce_sum 对矩阵的列求和，使用 axis=1 对矩阵的行求和，返回的结果降低一个维度。

import tensorflow as tf

x = tf.constant([[1, 2, 3],
                 [4, 5, 6]])

print(tf.reduce_sum(x, axis=0))
print(tf.reduce_sum(x, axis=1))

程序运行结果如下：

tf.Tensor([5 7 9], shape=(3,), dtype=int32)
tf.Tensor([ 6 15], shape=(2,), dtype=int32)

注意使用 axis 时指定操作的方向不能越界，也就是说你给定的是二维数组指定的方向只能为 0 或者 1，如果让 axis=2 则会越界报错，以下代码会报错。

import tensorflow as tf

x = tf.constant([[1, 2, 3],
                 [4, 5, 6]])

print(tf.reduce_sum(x, axis=2))  # 越界报错

如果我们给定一个三维张量，则可以指定操作的方向为 2，代码和结果如下图。我们发现使用 axis 是指定操作方向时，返回的结果的维度减一。

import tensorflow as tf

x = tf.constant([[[1, 2, 3]],
                 [[4, 5, 6]]])

print(tf.reduce_sum(x, axis=0))
print(tf.reduce_sum(x, axis=1))
print(tf.reduce_sum(x, axis=2))

程序运行结果如下：

tf.Tensor([[5 7 9]], shape=(1, 3), dtype=int32)
tf.Tensor(
[[1 2 3]
 [4 5 6]], shape=(2, 3), dtype=int32)
tf.Tensor(
[[ 6]
 [15]], shape=(2, 1), dtype=int32)

神经网络在训练时是把特征值和标签值配对后喂入网络，tf给出了把特征值和标签值配对的函数 tf.data.Dataset.from_tensor_slices（（特征值，标签值）），该函数支持 numpy 类型数据和 tensor 格式数据。

import tensorflow as tf

features = tf.constant([0.568, 0.779, 0.223, 0.099, 0.974])
labels = tf.constant([1, 1, 0, 0, 1])
dataset = tf.data.Dataset.from_tensor_slices((features, labels))

for item in dataset:
    print(item)

程序运行结果如下：

(<tf.Tensor: shape=(), dtype=float32, numpy=0.568>, <tf.Tensor: shape=(), dtype=int32, numpy=1>)
(<tf.Tensor: shape=(), dtype=float32, numpy=0.779>, <tf.Tensor: shape=(), dtype=int32, numpy=1>)
(<tf.Tensor: shape=(), dtype=float32, numpy=0.223>, <tf.Tensor: shape=(), dtype=int32, numpy=0>)
(<tf.Tensor: shape=(), dtype=float32, numpy=0.099>, <tf.Tensor: shape=(), dtype=int32, numpy=0>)
(<tf.Tensor: shape=(), dtype=float32, numpy=0.974>, <tf.Tensor: shape=(), dtype=int32, numpy=1>)

上面代码中我们给定五个特征值和五个标签值，然后让每个特征值和标签进行配对，然后我们遍历输出每个配对的结果，每个配对的结果都是一个 tensor。

tf.data.Dataset.from_tensor_slices（（特征值，标签值））.batch(配对数），我们加上 batch 函数可以指定配对数。

import tensorflow as tf

features = tf.constant([0.568, 0.779, 0.223, 0.099, 0.974])
labels = tf.constant([1, 1, 0, 1, 0])
dataset = tf.data.Dataset.from_tensor_slices((features, labels)).batch(2)

for item in dataset:
    print(item)

程序运行结果如下：

(<tf.Tensor: shape=(2,), dtype=float32, numpy=array([0.568, 0.779], dtype=float32)>, <tf.Tensor: shape=(2,), dtype=int32, numpy=array([1, 1])>)
(<tf.Tensor: shape=(2,), dtype=float32, numpy=array([0.223, 0.099], dtype=float32)>, <tf.Tensor: shape=(2,), dtype=int32, numpy=array([0, 1])>)
(<tf.Tensor: shape=(1,), dtype=float32, numpy=array([0.974], dtype=float32)>, <tf.Tensor: shape=(1,), dtype=int32, numpy=array([0])>)

由于我们设定了配对数为 2，我们发现 features 中的值和 labels 中的值是按照两两配对的方案，最后不够配对数的，作为一个整体配对。

可利用 tf 的 assign_sub 函数对参数实现自更新，也就是自减一运算。使用此函数前需利用 tf.Variable 定义变量 w 为可训练(可自更新)。

import tensorflow as tf

w = tf.Variable(4)
w.assign_sub(1)  # w = w -1

print(w)

程序运行结果如下：

<tf.Variable 'Variable:0' shape=() dtype=int32, numpy=3>

可利用 tf.argmax (张量名,axis=操作轴)返回张量沿指定维度最大值的索引。

import tensorflow as tf
import numpy as np

test = np.array([[1, 2, 3],
                 [2, 3, 4],
                 [3, 4, 5],
                 [5, 6, 7]])

print(tf.argmax(test, axis=0))  # 返回每一列（经度）最大值的索引
print(tf.argmax(test, axis=1))  # 返回每一行（纬度）最大值的索引

程序运行结果如下：

tf.Tensor([3 3 3], shape=(3,), dtype=int64)
tf.Tensor([2 2 2 2], shape=(4,), dtype=int64)

tf 的 where(条件语句，真返回 A，假返回 B)函数，该函数可以从两个张量中取出符合条件为真的元素组成一个张量返回给用户。

import tensorflow as tf

a = tf.constant([1, 2, 3, 1, 2])
b = tf.constant([0, 1, 3, 2, 4])
c = tf.where(tf.greater(a, b), a, b)  # 若 a > b，返回 a 对应位置的元素，否则返回 b 对应位置的元素

print("c:", c)

程序运行结果如下：

c: tf.Tensor([1 2 3 2 4], shape=(5,), dtype=int32)

上述代码中，我们用 greater 函数判断 a 和 b 两个张量的元素的小，如果 a 张量对应的元素大于 b张量对应的元素则返回 True，否则返回 False。如果 greater 函数返回 True，where 函数取 a 对应的元素，否则 where 函数取出 b 对应的元素。

tf 的 GradientTape 函数实现某个函数对指定参数的求导运算，该函数返回一个对象，调用该对象的 gradient（函数，对谁求导）既可以求出导数。

import tensorflow as tf

with tf.GradientTape() as tape:
    w = tf.Variable(tf.constant(3.0))
    loss = tf.pow(w, 2)  # loss = w ** 2

grad = tape.gradient(loss, w)

print(grad)

程序运行结果如下：

tf.Tensor(6.0, shape=(), dtype=float32)

如上代码，我们假定损失函数 loss = w²，我们知道 loss 对 w 求导为 2w，我们给定 w 值为 3.0，然后我们使用 gradient 函数计算 loss 对 w 的求导的值，得到结果为 6.0。

独热码

对于分类问题，我们得出的结果想以所有可能分类结果的概率的形式展现（独热码 one-hot），这样更清晰明了。

比如，我们使用神经网络来分类鸢尾花是属于哪一种类（标签 0 表示是狗尾草鸢尾花，标签 1 表示是杂色鸢尾花，标签 2 表示是弗吉尼亚鸢尾花），如果分类的结果为标签 1，我们知道是杂色鸢尾花，我们使用独热码的形式表示也就是以概率的形式表示，用独热码（0 1 0）来表示标签 1，这个独热码标签表示：0 狗尾草鸢尾花出现的概率为 0；1 杂色鸢尾花出现的概率为 1；2 弗吉尼亚鸢尾花出现的概率为 0；这样我们就可以得出该鸢尾花为 1 杂色鸢尾花。也就是说用独热码标签(0 1 0)代替了标签1会更清晰。

tf 的 one_hot（待转换数据，depth=几分类）函数将待转换数据标签转换为 one-hot 形式的数据标签输出。

import tensorflow as tf

classes = 3  # 3 分类
labels = tf.constant([1, 0, 2])  # 输入的标签值最小为 0，最大为 2
output = tf.one_hot(labels, depth=classes)  # 把原有标签转为独热码标签

print(output)

程序运行结果如下：

tf.Tensor(
[[0. 1. 0.]
 [1. 0. 0.]
 [0. 0. 1.]], shape=(3, 3), dtype=float32)

由以上代码和结果我们发现我们把 3 分类标签 [1, 0, 2] 中的标签 1 转为了独热码标签 [0. 1. 0.]，这个独热码 [0. 1. 0.] 表示 0 标签出现的概率为 0；1 标签出现的概率为 1； 2 标签出现的概率为 0，所以这个值也就是标签 1。同理把标签 0 转为了独热码标签 [1. 0. 0.]，把标签 2 转为了独热码标签 [0. 0. 1.]。

最后注意两点：第一，转为独热码是以浮点数形式表示；第二，独热码中的所有元素表示的是每个分类出现的概率，总和为 1。

我们在做神经网络训练时，要把前向传播的结果转为符合概率分布的数值后才能和独热码标签做比较，tf 的 softmax 函数可以把标签结果转为符合概率分布的数值。

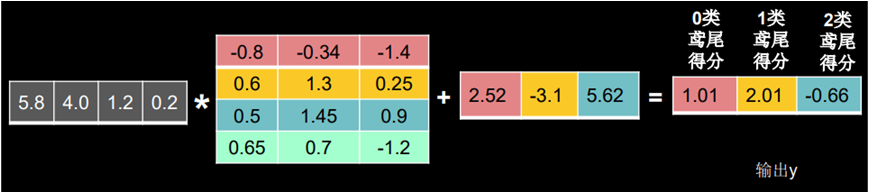
如上图鸢尾花分类问题，我们通过神经网络前向传播后的值分别为 1.01、2.01、-0.66，这个值明显不符合独热码的特性，我们可以使用 tf.nn.softmax 函数使前向传播的输出值符合概率分布，进而与独热码形式的标签作比较，其计算公式为 $\frac{e^{y_i}}{{\mathrm{\Sigma \; <!--\; greek\; capital\; letter\; sigma\; -->}}_{j=0}^n{e}^{yj}}$，其中 $y_i$ 是前向传播的输出。

通过上述计算公式，可计算对应的概率值：

$\frac{e^{y_0}}{e^{y_0}+e^{y_1}+e^{y_2}}$

$\frac{e^{y_1}}{e^{y_0}+e^{y_1}+e^{y_2}}$

$\frac{e^{y_2}}{e^{y_0}+e^{y_1}+e^{y_2}}$

上式中，0.256 表示为 0 类鸢尾的概率是 25.6%；0.695 表示为 1 类鸢尾的概率是 69.5%；0.048 表示为 2 类鸢尾的概率是 4.8%。

import tensorflow as tf

y = tf.constant([1.01, 2.01, -0.66])
y_pro = tf.nn.softmax(y)

print("After softmax, y_pro is:", y_pro)

程序运行结果如下：

After softmax, y_pro is: tf.Tensor([0.25598174 0.69583046 0.04818781], shape=(3,), dtype=float32)

我们通过 softmax 函数把标签值 [1.01, 2.01, -0.66] 转为了符合独热码格式的 [0.25598174, 0.69583046, 0.0481878]，该值的每个元素符合落在 [0, 1) 区间，且总和为 1。

本节重要知识点

熟练掌握这些函数的意义

熟练使用这些函数

如果以上内容对您有帮助，请老板用微信扫一下赞赏码，赞赏后加微信号 birdpython 领取免费视频。