



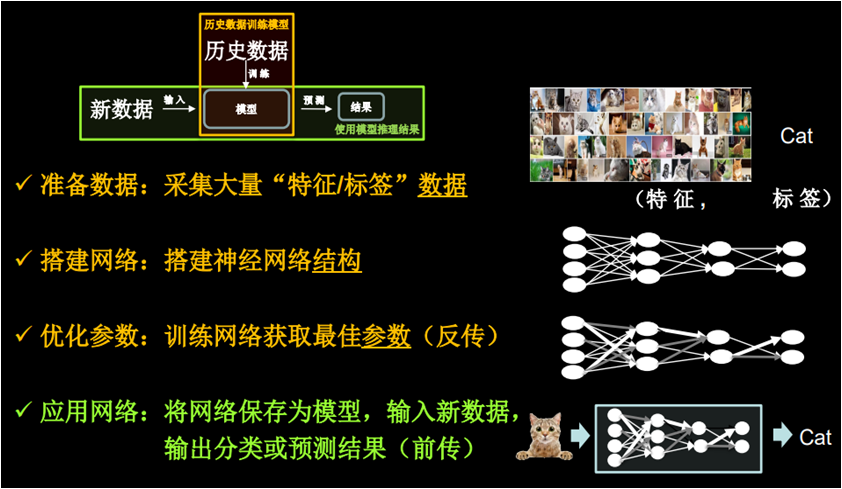
神经网络设计过程
阅读:1332958376 分享到我们用计算机仿出人的神经网络连接关系,让计算机具备感性思维。首先需要准备数据,数据量越大越好,要构成特征和标签对,如果我们构建一个可以识别猫的神经网络,就要有大量猫的图片和这张图片是猫的标签,构成特征和标签对,然后搭建神经网络的网络结构,再后,通过反向传播优化连接的权重,直到模型的识别准确率达到要求,得到具有最优连接权重的神经网络,然后把这个模型保存起来,然后我们就可以给该模型输入从未见过的新数据,他会通过前向传播输出概率值 ,概率值最大的那个就是分类和预测的结果了。
人工神经网络的设计过程如下:
1.准备数据集,提取特征,作为输入喂入神经网络(数据集)
2.搭建神经网络结构,从输入到输出(前向传播)
3.大量特征数据喂入神经网络, 通过损失函数,梯度下降,学习率等知识迭代优化神经网络参数(反向传播)
4.使用训练好的模型预测和分类(使用模型)
搭建神经网络
人工神经网络的搭建过程如下图:
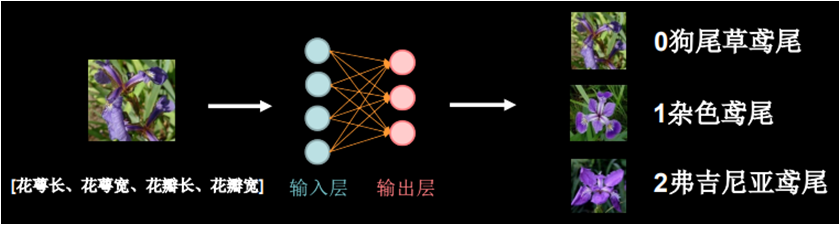
我们举个列子来学习神经网络的设计过程,下面我们搭建一个能给鸢尾花分类的神经网络,鸢尾花共有三类,如下图:

然后我们搭建一个神经网络模型用来识别任意一个用户给出的鸢尾花是属于哪一类。

人们通过经验总结出了规律:通过测量花的花萼长、花萼宽、花瓣长、花瓣宽,可以得出鸢尾花的类别。(如:花萼长>花萼宽 且 花瓣长/花瓣宽>2 则为 1杂色鸢尾)
对于上面我们给出的判断条件,我们使用 if 等条件判断语句就可以实现鸢尾花的分类了,条件语句根据这些信息是可以判断鸢尾花的分类,这个过程是理性的计算,只要根据这些判断条件,我们一定可以通过条件判断语句计算出是哪类鸢尾花,这是识别方式这是一个非常典型的专家系统,这属于传统的人工智能(符号主义)。

但是我们平时在识别鸢尾花的时候并不需要这么理性的计算,如果我们见识了太多的鸢尾花,一眼就能看出是那种,而且随着经验的增加,识别的准确率就会越来越精确,这就是直觉,也就是人的感性思维, 这种靠感性思维识别的方法就是依靠人的神经网络。在此,我们要搭建的人工神经网络,然后培养出感性思维来识别鸢尾花。搭建识别鸢尾花神经网络的设计过程如下。

首先,我们需要采集大量的花萼长、花萼宽、花瓣长、花瓣宽和他们所对应的是那种鸢尾花类别,花萼长、花萼宽、花瓣长、花瓣宽我们叫做输入特征,他们对应的分类我们叫做标签。
大量的输入特征和标签对构建出数据集,我们把这些数据集喂入搭建好的神经网络结构,然后神经网络通过反向传播优化参数得到模型,当有新的从未见过的输入特征送入我们的神经网络模型时,神经网络就能识别出结果。
下面我们看一下用神经网络实现鸢尾花分类的具体实现过程。
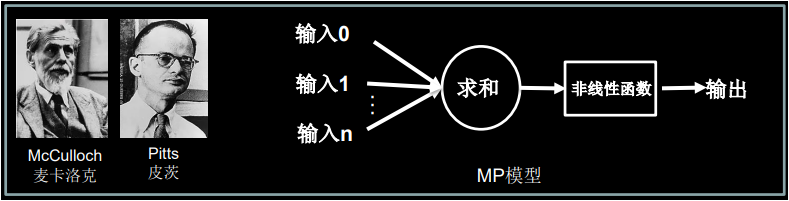
首先输入的特征是:花萼长、花萼宽、花瓣长、花瓣宽,这是一个 1 行 4 列的数据,通过一个神经网络输出的是每个种类的可能性大小,这个神经网络里的每一个具有计算功能的粉色小球就是一个神经元。
早在 1943 年,英国心理学家麦卡洛克和数学家皮茨就给出了神经元的计算模型,该模型叫做 MP 模型,MP 模型是每个输入特征乘以线上的权重求和,然后在通过一个非线性函数输出。
为了求解简单,我们暂时去掉非线性函数,我们把MP模型简化成下面这个样子。
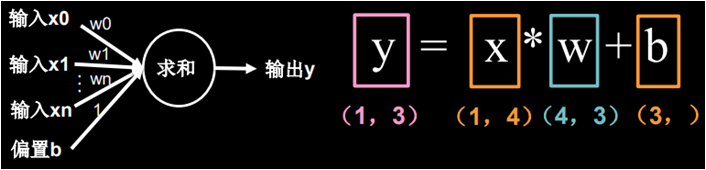
也就是把所有输入 x 叉乘以各自线上的权重w求和加上偏置项 b 输出 y,写成数学公式的样子也就是:y = x叉乘w + b
针对我们鸢尾花的例子,输入特征 x 是 1 行 4 列的矩阵,线上权重 w 是 4 行 3 列的矩阵(为了支持矩阵叉乘,w 矩阵的行要等于 x 矩阵的列,所以行是 4;w 矩阵的列要等于 y 矩阵的列,所以列是 3),偏置项 b 是含有 3 个元素的向量,输出标签 y 是 1 行 3 列的矩阵,这个 y 就是三种鸢尾花各自的可能性大小。
为了求解简单,我们暂时去掉非线性函数,我们把 MP 模型简化成下面这个样子。
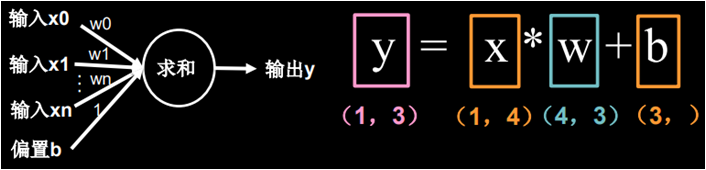
也就是把所有输入 x 叉乘以各自线上的权重 w 求和加上偏置项 b 输出 y,写成数学公式的样子也就是:y = x叉乘w + b
针对我们鸢尾花的例子,输入特征 x 是 1 行 4 列的矩阵,线上权重 w 是 4 行 3 列的矩阵(为了支持矩阵叉乘,w 矩阵的行要等于 x 矩阵的列,所以行是 4;w 矩阵的列要等于 y 矩阵的列,所以列是 3),偏置项 b 是含有 3 个元素的向量,输出标签 y 是 1 行 3 列的矩阵,这个 y 就是三种鸢尾花各自的可能性大小。
数据集输入
我们已经分析了神经网络整个构造流程,现在就让我们开始搭建神经网络吧。
输入是花萼长、花萼宽、花瓣长、花瓣宽这 4 个特征,所以我们的输入有 4 个节点(x0 、x1 x2 、x3);输出是 3 中鸢尾花各自的可能性大小,所以我们的输出有个 3 个节点(y0 、y1 、y2);中间连线有4行3列,线上的权重w一共12个;每个神经元还有一个偏置项b,我们可以根据以上条件搭建出神经网络结构如下。
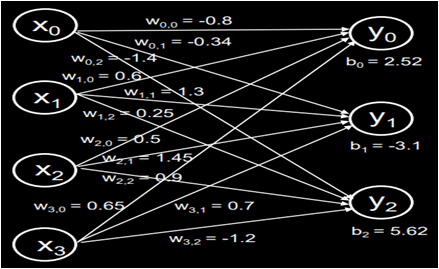
里面的每个神经元(y0、y1、y2)和前面一层的每个节点(x0、x1、x2、x3)都有连接关系,我们称之为全连接网络,有了这个神经网络结构,线上的权重 w 和偏置 b 会被随机初始化为一些随机数,我们喂入一组鸢尾花的输入特征(5.8、4.0、1.2、0.2)和他们对应的标签(0 狗尾草鸢尾花)
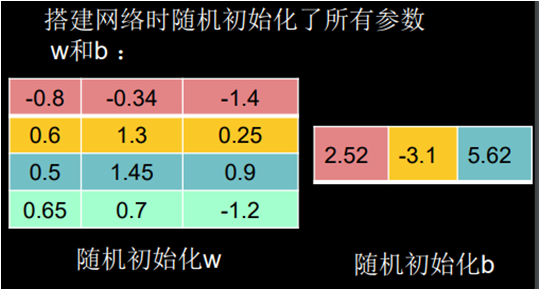
前向传播
神经网络按照公式 y = x叉乘w + b ,根据已知的输入数据x和随机初始化的权重 w 以及随机初始化的偏置 b 计算出 y,这个过程就叫前向传播。
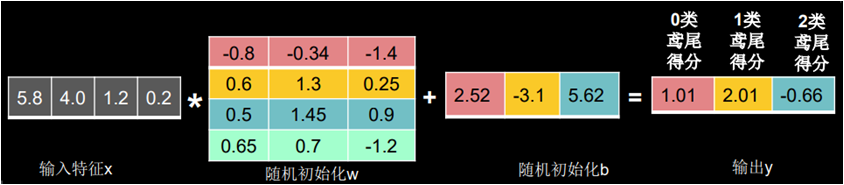
通过输出的 y 值可以看出我们的神经网络得到可能性最高的是 1 类鸢尾花,而不是标签 0 类鸢尾花,这是因为公式 y = x叉乘w + b中的参数 w 和 b 都是我们随机给的,根据这个随机的 w 值和 b 值计算出的结果 y 就是瞎蒙的。也就是说我们目前的神经网络还没有见过鸢尾花,它还没有判断鸢尾花类别相关的智能。我们需要给他喂入大量的鸢尾花数据(输入特征)以及告知它这是什么鸢尾花(标签)来不断的调整 w 和 b,最终让它具有识别鸢尾花类别的智能。
损失函数
我们用损失函数定义预测值 y 和真实结果也就是标签 y_ 的差距,损失函数可以定量地判断当前这组参数 w 和 b 的优劣,从而让我们得到最优的 w 和 b 的值,因为损失函数表达的是预测值与真实结果之间的差距,当损失函数的结果最小时,参数 w 和 b 会出现最优值。
在讲解线性回归时,我们已经详细了解了损失函数相关知识,我们知道损失函数定义有很多方法,均方误差就是一种常用的损失函数。

梯度下降
我们的目的是要寻找一组参数 w 和 b 使得损失函数值最小,损失函数的梯度表示损失函数对各参数求偏导后的向量,损失函数梯度下降的方向就是损失函数减小的方向,梯度下降就是沿着损失函数梯度下降的方向寻找损失函数的极小值(注意有可能不是最小值,所以有可能陷入局部极小从而找不到最小值,我们暂且忽略损失函数有个多个极小值的可能,如果损失函数只有一个极小值,则这个极小值就是最小值),从而得到最优的参数 w 和 b。如下图,左边曲线是损失函数,右边是按梯度下降法更新参数的计算。

学习率
上面计算公式中,lr 是学习率也就是梯度下降的速度,它是一个超参数,如果设置学习率过小,参数更新会很慢,如果学习率设置过大,参数更新会跳过最小值,随意这个超参数我们要根据实际情况进行调整。

反向传播
现在我们举个例子来体会一下反向传播的过程,假设损失函数的公式为:,我们知道损失函数对参数 w 的偏导为:2w + 2。
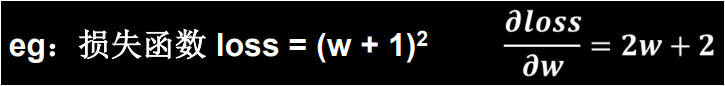
对于参数 w 我们一开始随机初始化一个随机值假定为 5,我们设定超参数学习率为 0.2,按照公式:,我们的计算过程如下。
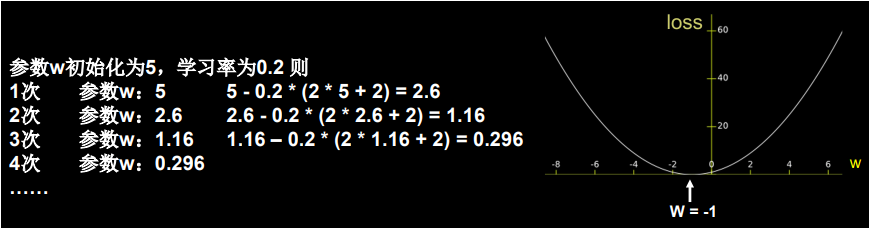
我们通过该损失函数对应的几何图形可以看出,优化参数 w 就是不停的更改 w 值使得损失函数的梯度一直减小。因为我们初始化 w 为随机值 5,w = 5对应的损失函数值为 36,我们从图形上可以看出,损失函数 loss 的极小值(对该函数来说这个极小值也是最小值)应该为 0,而 loss = 0 对应的 w 为 -1,现在我们就通过不停的减小 w 找到损失函数 loss 的最小值 0,从而得出最优的 w。下面我们通过代码来体验一下通过反向传播,梯度下降使损失函数减小,参数更新的过程。
import tensorflow as tf w = tf.Variable(5, dtype=tf.float32) # 我们给w随机初始化一个值5.0 lr = 0.2 # 给定超参数学习率的值,该值是个经验值,可以根据后续训练的情况做调整 epoch = 40 # 学习训练40次 for step in range(epoch): # 迭代更新40次 with tf.GradientTape() as tape: loss = tf.square(w + 1) # 定义损失函数 loss=(w+1)² grads = tape.gradient(loss, w) # gradient函数让loss对w求导 w.assign_sub(lr * grads) # 更新w,使得:w = w -lr(∂loss/∂w) print("第 %s 次迭代后的w是 %f,对应的loss值是 %f" % (step, w.numpy(), loss))
当 lr 设定为 0.2 时,我们看下程序执行的结果。
第 0 次迭代后的w是 2.600000,对应的loss值是 36.000000 第 1 次迭代后的w是 1.160000,对应的loss值是 12.959999 第 2 次迭代后的w是 0.296000,对应的loss值是 4.665599 第 3 次迭代后的w是 -0.222400,对应的loss值是 1.679616 第 4 次迭代后的w是 -0.533440,对应的loss值是 0.604662 第 5 次迭代后的w是 -0.720064,对应的loss值是 0.217678 第 6 次迭代后的w是 -0.832038,对应的loss值是 0.078364 第 7 次迭代后的w是 -0.899223,对应的loss值是 0.028211 第 8 次迭代后的w是 -0.939534,对应的loss值是 0.010156 第 9 次迭代后的w是 -0.963720,对应的loss值是 0.003656 第 10 次迭代后的w是 -0.978232,对应的loss值是 0.001316 第 11 次迭代后的w是 -0.986939,对应的loss值是 0.000474 第 12 次迭代后的w是 -0.992164,对应的loss值是 0.000171 第 13 次迭代后的w是 -0.995298,对应的loss值是 0.000061 第 14 次迭代后的w是 -0.997179,对应的loss值是 0.000022 第 15 次迭代后的w是 -0.998307,对应的loss值是 0.000008 第 16 次迭代后的w是 -0.998984,对应的loss值是 0.000003 第 17 次迭代后的w是 -0.999391,对应的loss值是 0.000001 第 18 次迭代后的w是 -0.999634,对应的loss值是 0.000000 第 19 次迭代后的w是 -0.999781,对应的loss值是 0.000000 第 20 次迭代后的w是 -0.999868,对应的loss值是 0.000000 第 21 次迭代后的w是 -0.999921,对应的loss值是 0.000000 第 22 次迭代后的w是 -0.999953,对应的loss值是 0.000000 第 23 次迭代后的w是 -0.999972,对应的loss值是 0.000000 第 24 次迭代后的w是 -0.999983,对应的loss值是 0.000000 第 25 次迭代后的w是 -0.999990,对应的loss值是 0.000000 第 26 次迭代后的w是 -0.999994,对应的loss值是 0.000000 第 27 次迭代后的w是 -0.999996,对应的loss值是 0.000000 第 28 次迭代后的w是 -0.999998,对应的loss值是 0.000000 第 29 次迭代后的w是 -0.999999,对应的loss值是 0.000000 第 30 次迭代后的w是 -0.999999,对应的loss值是 0.000000 第 31 次迭代后的w是 -1.000000,对应的loss值是 0.000000 第 32 次迭代后的w是 -1.000000,对应的loss值是 0.000000 第 33 次迭代后的w是 -1.000000,对应的loss值是 0.000000 第 34 次迭代后的w是 -1.000000,对应的loss值是 0.000000 第 35 次迭代后的w是 -1.000000,对应的loss值是 0.000000 第 36 次迭代后的w是 -1.000000,对应的loss值是 0.000000 第 37 次迭代后的w是 -1.000000,对应的loss值是 0.000000 第 38 次迭代后的w是 -1.000000,对应的loss值是 0.000000 第 39 次迭代后的w是 -1.000000,对应的loss值是 0.000000
通过以上结果,我们可以看到 w 值和 loss 值的变化,我们经过第 18 轮更新迭代 w 就得到了 loss 的最小值 0,从而得到最优的 w 值为 -1,这样我们就得到了最优的神经网络模型。
当 lr 设定为 0.001 时,我们看下程序执行的结果。
第 0 次迭代后的w是 4.988000,对应的loss值是 36.000000 第 1 次迭代后的w是 4.976024,对应的loss值是 35.856144 第 2 次迭代后的w是 4.964072,对应的loss值是 35.712864 第 3 次迭代后的w是 4.952144,对应的loss值是 35.570156 第 4 次迭代后的w是 4.940240,对应的loss值是 35.428020 第 5 次迭代后的w是 4.928360,对应的loss值是 35.286449 第 6 次迭代后的w是 4.916503,对应的loss值是 35.145447 第 7 次迭代后的w是 4.904670,对应的loss值是 35.005009 第 8 次迭代后的w是 4.892860,对应的loss值是 34.865124 第 9 次迭代后的w是 4.881075,对应的loss值是 34.725803 第 10 次迭代后的w是 4.869313,对应的loss值是 34.587044 第 11 次迭代后的w是 4.857574,对应的loss值是 34.448833 第 12 次迭代后的w是 4.845859,对应的loss值是 34.311172 第 13 次迭代后的w是 4.834167,对应的loss值是 34.174068 第 14 次迭代后的w是 4.822499,对应的loss值是 34.037510 第 15 次迭代后的w是 4.810854,对应的loss值是 33.901497 第 16 次迭代后的w是 4.799233,对应的loss值是 33.766029 第 17 次迭代后的w是 4.787634,对应的loss值是 33.631104 第 18 次迭代后的w是 4.776059,对应的loss值是 33.496712 第 19 次迭代后的w是 4.764507,对应的loss值是 33.362858 第 20 次迭代后的w是 4.752978,对应的loss值是 33.229538 第 21 次迭代后的w是 4.741472,对应的loss值是 33.096756 第 22 次迭代后的w是 4.729989,对应的loss值是 32.964497 第 23 次迭代后的w是 4.718529,对应的loss值是 32.832775 第 24 次迭代后的w是 4.707092,对应的loss值是 32.701576 第 25 次迭代后的w是 4.695678,对应的loss值是 32.570904 第 26 次迭代后的w是 4.684287,对应的loss值是 32.440750 第 27 次迭代后的w是 4.672918,对应的loss值是 32.311119 第 28 次迭代后的w是 4.661572,对应的loss值是 32.182003 第 29 次迭代后的w是 4.650249,对应的loss值是 32.053402 第 30 次迭代后的w是 4.638949,对应的loss值是 31.925320 第 31 次迭代后的w是 4.627671,对应的loss值是 31.797745 第 32 次迭代后的w是 4.616416,对应的loss值是 31.670683 第 33 次迭代后的w是 4.605183,对应的loss值是 31.544128 第 34 次迭代后的w是 4.593973,对应的loss值是 31.418077 第 35 次迭代后的w是 4.582785,对应的loss值是 31.292530 第 36 次迭代后的w是 4.571619,对应的loss值是 31.167484 第 37 次迭代后的w是 4.560476,对应的loss值是 31.042938 第 38 次迭代后的w是 4.549355,对应的loss值是 30.918892 第 39 次迭代后的w是 4.538256,对应的loss值是 30.795341
通过以上结果,我们发现学习率过小时,梯度下降的跨度很小,参数更新很慢,我们经过 40 轮更新迭代未能找到 loss 的最小值。
当 lr 设定为 0.99 时,我们看下程序执行的结果。
通过以上结果,我们发现学习率过大时,参数在最优值两边跳动,这样无论训练多少次也找不到 loss 的最小值。
第 0 次迭代后的w是 -6.880000,对应的loss值是 36.000000 第 1 次迭代后的w是 4.762401,对应的loss值是 34.574402 第 2 次迭代后的w是 -6.647153,对应的loss值是 33.205261 第 3 次迭代后的w是 4.534210,对应的loss值是 31.890335 第 4 次迭代后的w是 -6.423526,对应的loss值是 30.627483 第 5 次迭代后的w是 4.315056,对应的loss值是 29.414633 第 6 次迭代后的w是 -6.208755,对应的loss值是 28.249819 第 7 次迭代后的w是 4.104580,对应的loss值是 27.131124 第 8 次迭代后的w是 -6.002488,对应的loss值是 26.056736 第 9 次迭代后的w是 3.902438,对应的loss值是 25.024887 第 10 次迭代后的w是 -5.804390,对应的loss值是 24.033899 第 11 次迭代后的w是 3.708302,对应的loss值是 23.082163 第 12 次迭代后的w是 -5.614137,对应的loss值是 22.168112 第 13 次迭代后的w是 3.521854,对应的loss值是 21.290257 第 14 次迭代后的w是 -5.431417,对应的loss值是 20.447166 第 15 次迭代后的w是 3.342790,对应的loss值是 19.637461 第 16 次迭代后的w是 -5.255934,对应的loss值是 18.859821 第 17 次迭代后的w是 3.170815,对应的loss值是 18.112972 第 18 次迭代后的w是 -5.087399,对应的loss值是 17.395702 第 19 次迭代后的w是 3.005651,对应的loss值是 16.706835 第 20 次迭代后的w是 -4.925539,对应的loss值是 16.045244 第 21 次迭代后的w是 2.847028,对应的loss值是 15.409853 第 22 次迭代后的w是 -4.770087,对应的loss值是 14.799623 第 23 次迭代后的w是 2.694685,对应的loss值是 14.213558 第 24 次迭代后的w是 -4.620792,对应的loss值是 13.650701 第 25 次迭代后的w是 2.548376,对应的loss值是 13.110134 第 26 次迭代后的w是 -4.477408,对应的loss值是 12.590973 第 27 次迭代后的w是 2.407860,对应的loss值是 12.092369 第 28 次迭代后的w是 -4.339703,对应的loss值是 11.613512 第 29 次迭代后的w是 2.272909,对应的loss值是 11.153617 第 30 次迭代后的w是 -4.207451,对应的loss值是 10.711934 第 31 次迭代后的w是 2.143302,对应的loss值是 10.287741 第 32 次迭代后的w是 -4.080436,对应的loss值是 9.880347 第 33 次迭代后的w是 2.018827,对应的loss值是 9.489084 第 34 次迭代后的w是 -3.958450,对应的loss值是 9.113317 第 35 次迭代后的w是 1.899282,对应的loss值是 8.752428 第 36 次迭代后的w是 -3.841296,对应的loss值是 8.405833 第 37 次迭代后的w是 1.784470,对应的loss值是 8.072962 第 38 次迭代后的w是 -3.728781,对应的loss值是 7.753273 第 39 次迭代后的w是 1.674205,对应的loss值是 7.446244
我们总结一下:
我们准备更新迭代 40 次来调整 w 的值让 loss 值减小,由于学习率 lr 的值或者 loss 函数本身的问题,如果 lr 设置恰当,我们有可能不到 40 次就找到 loss 的最小值;也有可能 lr 设置过小,我们在 40 次以内不一定找到 loss 的最小值;也有可能 lr 设置过大,梯度下降的跨度太大从而跳过最小值,这样无论多少次也找不到最小值;也有可能损失函数 loss 的最小值是无穷小,我们无论训练多少次都找不到 loss 的最小值。
注意,我们并不是必须要找到 loss 的最小值,我们的目的是优化神经网络。但是对于该损失函数 ,我们只要学习率设置恰当,训练次数给的足够,是能找到最小值 loss = 0 的。
本节重要知识点
了解人工神经网络的定义
了解人工神经网络设计过程
了解人工神经网络涵盖的知识点





